Energy band theory is a basis for describing processes and effects in solid crystals under electromagnetic field impact Energy band theory is a theory of a valence electron moving in a periodic potential field of a crystalline lattice Single atoms have a discrete energy spectrum, which means they can occupy only discrete energy levels The Berry phase of π in graphene is derived in a pedagogical way The ambiguity of how to calculate this value properly is clarified Its connection with the unconventional quantum Hall effect in graphene is discussed•Dynamics of Electrons in Energy Bands II MJ Gilbert ECE 535 – Lecture 18 Berry'S phase The extra phase factor is called the Berry's phase and appears in many places in hysics (and in optics) solid state physics (spin Hall effect for example)

Electronic Band Structure An Overview Sciencedirect Topics
Berry phase for energy bands in solids
Berry phase for energy bands in solids- Berry phase and Berry curvature have become ubiquitous concepts in physics, relevant to a variety of phenomena, such as polarization, various Hall effects, etc Studies of these phenomena call for7 Berry phase for itinerant electrons in a solid 19 Berry phase, which had been overlooked for more than half a century, provides us a very deep insight on the geometric structure of quantum mechanics and gives rise to various observable effects The concept of the Berry has now become a central unifying concept in quantum me
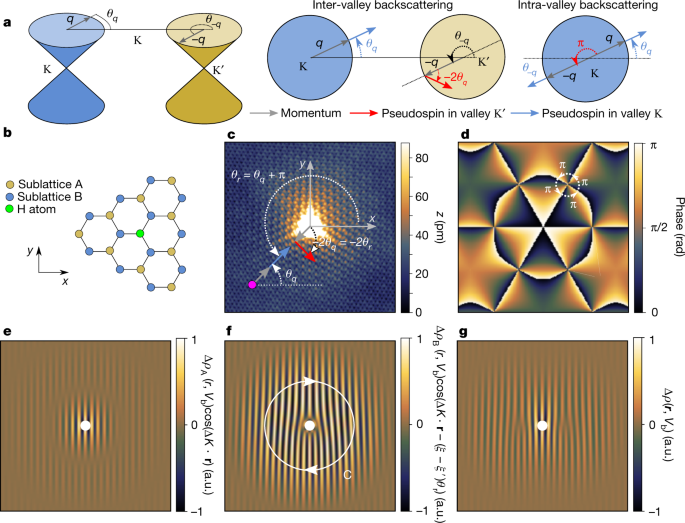



Measuring The Berry Phase Of Graphene From Wavefront Dislocations In Friedel Oscillations Nature
Berry phase and Berry curvature in solids Justin Song Nanyang Technological University, SingaporeМіжнародна школаконференція з проблем квантового It is very easy to forecast what happend in a phase transition from a gas to a system even more interacting like a liquid or a solid The result you can argue with me is that the degeneration in the energy spectrum is defintely removed and the energy levels (lines in spectrum) are much less intense and narrow Energy band theory of solids 1 PREPARED BY Baranitharan Kings College of Engineering 2 Nomenclature For most purposes, it is sufficient to know the En(k) curves the dispersion relations along the major directions of the reciprocal lattice
Electronic Band Structure of Crystals 41 Energy Bands in Solids 411 Bloch's theorem The Hamiltonian for an electron in a crystal is H= − ~2 2m ∇2 V(r) , (41) where V(r) = V(r R) for all R ∈ L, where L is the direct Bravais lattice underlying the crystal structure The potential V(r) describes the crystalline potential due to the Berry's phase for energy bands in solids Berry's phase for energy bands in solids Berry's phase for energy bands in solids Phys Rev Lett 19 Jun 5;62(23) doi /PhysRevLett Author J Zak PMID DOIQuantum Geometric phase Berry Phase H(R(t)) M V Berry, ProcR Soc Lond A 392, 45 (1984) R(t) parameter space Eigenstate Geometric phase R* is the point where E m(R*)=E n(R*) with energy degeneracy or band crossing Magnetic monopole in Rspace around R* R*=0 E R Berry phase 1, accumulated phase along looppath C inside of vector
Finally, we expect that for a twodimensional case, by adding another orthogonal pulse after the splitting of the Bloch electron wavepacket, the Berry phase along a closed orbit in the reciprocal space may be measured Our proposal may find potential applications in imaging the properties of energy bands in solids AcknowledgmentsOver the past twentyfive years, mathematical concepts associated with geometric phases have come to occupy a central place in our modern understanding of the physics of electrons in solids These 'Berry phases' describe the global phase acquired by a quantum state as the Hamiltonian is changed Beginning at an elementary level, this book provides a pedagogical introduction to the The relationship between the energy and the crystal momentum of electrons is called the band structure of solids For electrons in solids, the Berry curvature and the quantum metric of Bloch



D Nb Info




Juelich Berry Phase In Solid State Physics
In solidstate physics, the electronic band structure (or simply band structure) of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have (called band gaps or forbidden bands) Band theory derives these bands and band gaps by examining the allowed quantum mechanical wave functions for an electron in aEnergy Band Theory According to Bohr's theory, every shell of an atom contains a discrete amount of energy at different levels Energy band theory explains the interaction of electrons between the outermost shell and the innermost shell Based on the energy band theory, there are three different energy bands Valence band Forbidden energy gapIn classical and quantum mechanics, geometric phase is a phase difference acquired over the course of a cycle, when a system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian The phenomenon was independently discovered by T Kato (1950), S Pancharatnam (1956), and by H C Longuet




Electronic Band Structure An Overview Sciencedirect Topics



Ens Lyon Fr
Electronic band structures dictate the mechanical, optical and electrical properties of crystalline solids Their experimental determination is therefore of crucial importance for technological applications While the spectral distribution in energy bands is routinely measured by various techniques, it is more difficult to access the topological properties of band structures such as the Berry8 Topological Insulators C d(k) FIGURE 2 The Berry phase in a two band theory is given by half the solid angle swept out by dˆ(k) It is useful to understand the Berry phase for the simplest two level Hamiltonian, which may be expressed in terms of Pauli matrices σ asThe quantum Hall effect is a famous example where the geometry of wave functions plays a crucial role in lowenergy transport The Hall conductivity σ xy can be represented by the integral of the Berry curvature F n (k) ≡ ∇ k × a n (k) z over the occupied states ()In the case of an insulator, the integral with respect to k over the first Brillouin zone is quantized and called the



Phy Ntnu Edu Tw
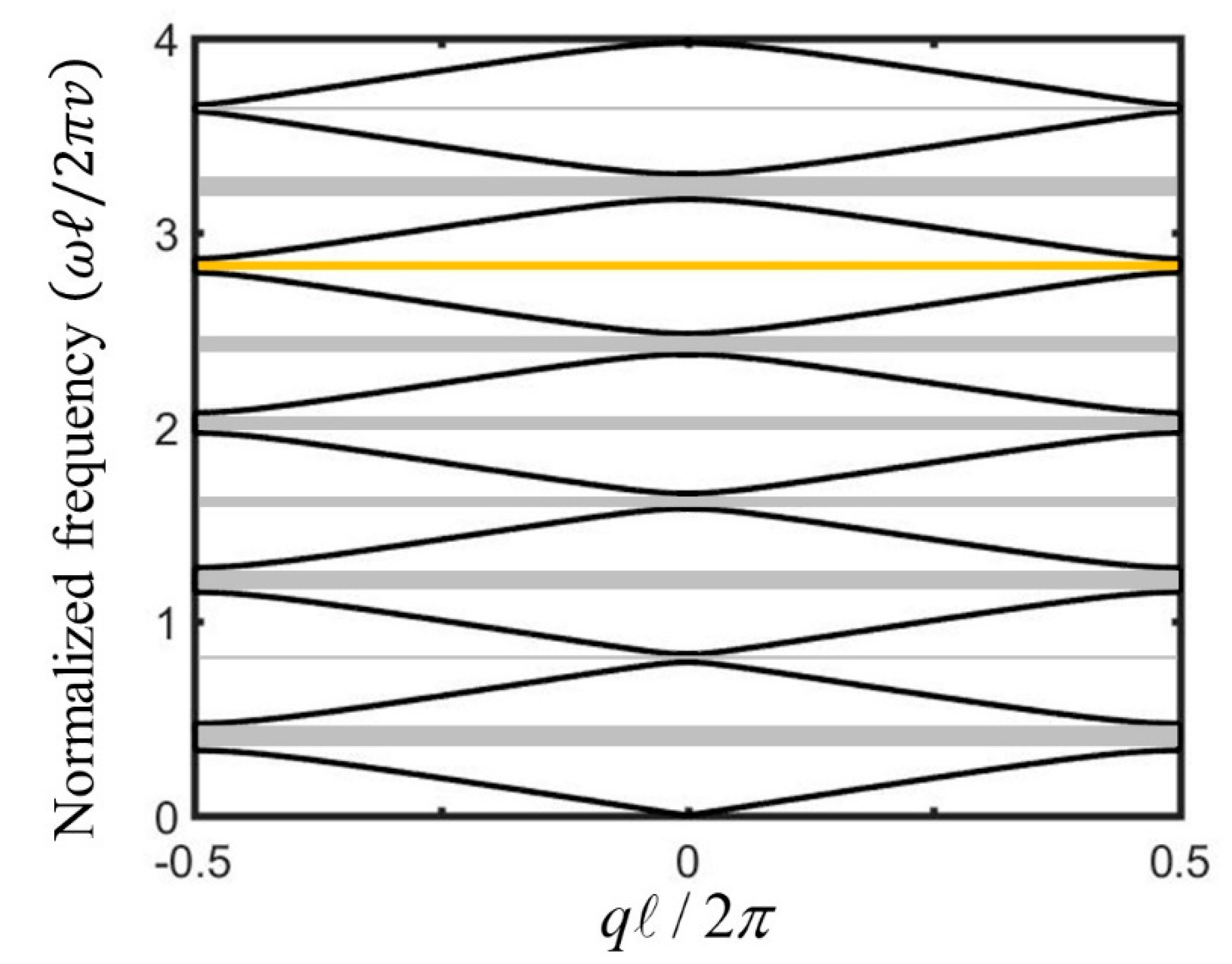



Crystals Free Full Text Topological Phase Transition In A One Dimensional Elastic String System Html
Band Theory of Solids A useful way to visualize the difference between conductors, insulators and semiconductors is to plot the available energies for electrons in the materials Instead of having discrete energies as in the case of free atoms, the available energy states form bandsCrucial to the conduction process is whether or not there are electrons in the conduction band If the Fermi energy is in this induced energy gap, this leads to a halfinteger quantized Hall conductivity σxy = (1/2)e2/h (Fig 2) due to the Berry's phase of π on the topological surface To induce such a gap, Tse and MacDonald propose to place a thick film of a topological insulator between two ferromagnetsAlthough the spectral distribution in energy bands is routinely measured by various techniques 1, it is more difficult to access the topological properties of band structures such as the quantized Berry phase, γ, which is a gaugeinvariant geometrical phase accumulated by the wavefunction along an adiabatic cycle 2



Energy Bands In Solids And Their Calculations Mse 5317
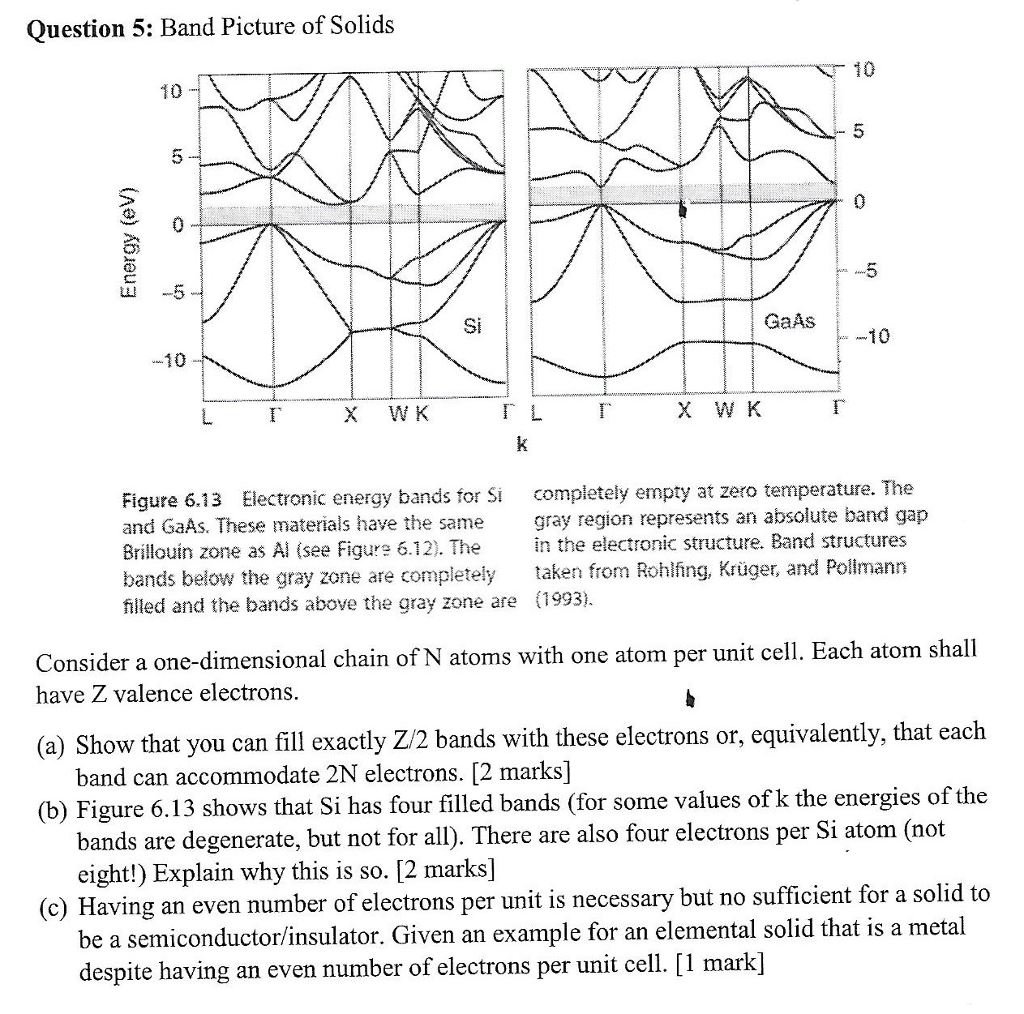



Solved Question 5 Band Picture Of Solids 10 10 5 Ul Si Gaas Chegg Com
The band theory of solids is different from the others because the atoms are arranged very close to each other such that the energy levels of the outermost orbital electrons are affected But the energy level of the innermost electrons is not affected by the neighbouring atoms The three energy bands in solids are Valence band; The relationship between the energy and the crystal momentum of electrons is called the band structure of solids For electrons in solids, the Berry curvature and the quantum metric of Bloch Berry's phase for energy bands in solids Zak, J Berry's phase is defined for the dynamics of electrons in periodic solids and an explicit formula is derived for it Because of the special torus topology of the Brillouin zone a nonzero Berry phase is shown to exist in a onedimensional parameter space



Arxiv Org



Rotating Polarization Using Berry S Phase In Asymmetric Silicon Strip Waveguides
Highorder sideband generation (HSG) is a highly nonlinear optical process HSG involves two frequencies of light relatively weak nearinfrared (NIR) light and very intense THz light When the two are combined in a highmobility semiconductor material, many new frequencies are created, as can be seen in Fig 118 Berry phase in condensed matter physics, a partial list 19 Quantized Hall conductance (Thouless et al) 19 Quantized charge transport (Thouless) 1984 Anyon in fractional quantum Hall effect (Arovas et al) 19 Berry phase in onedimensional lattice (Zak) 1990 Persistent spin current in onedimensional ring (Loss et al) 1992 Quantum tunneling in magnetic cluster (Loss et al)If this video helped you a lot then, instead of saying thank you, You can Subscribe my other youtube channel, it's a humble request🙏🙏Link below👇👇https//




Nanohub Org Resources Topological Materials As Platforms For New Particles And Electromagnetic Responses Watch Presentation



Wwwphy Princeton Edu
Adshelpatcfaharvardedu The ADS is operated by the Smithsonian Astrophysical Observatory under NASA Cooperative Agreement NNX16AC86AA Berry Phase of a Single Spin The classic example, which many of you may have seen, of Berry's phase is to consider a single spin in a time dependent magnetic field H = BS (514) We will let the direction of B in space be the control parameter of the Hamiltonian Starting with a reference state with spin projection m in the ˆz D Berry phase in Bloch bands 1965 II Adiabatic Transport and Electric Polarization 1966 This review concerns applications of the Berry phase concept in solidstate physics In this field, we are typically interested in macroscopic phenomena which is slow band energy in place of the freeparticle dispersion Be
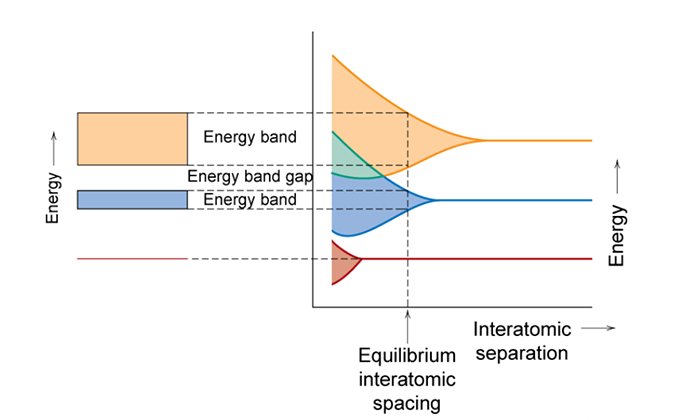



Energy Bands Matse 81 Materials In Today S World



Phy Ntnu Edu Tw
Examples of Energy Bands in Solids What we can find out see Mizutani for more details Metal is a solid with a Fermi surface!D Berry phase in Bloch bands 1965 II Adiabatic Transport and Electric Polarization 1966 This review concerns applications of the Berry phase concept in solidstate physics In this field, we are typically interested in macroscopic phenomena which is slow band energy in place of the freeparticle dispersion Be Abstract The geometric structure of a singleparticle energy band in a solid is fundamental for a wide range of manybody phenomena and is uniquely characterized by the distribution of Berry curvature over the Brillouin zone We realize an atomic interferometer to measure Berry flux in momentum space, in analogy to an AharonovBohm




Effect Of Spin Berry Phase A The Spin Berry Phase Wijk Is Equal To Download Scientific Diagram



D Nb Info
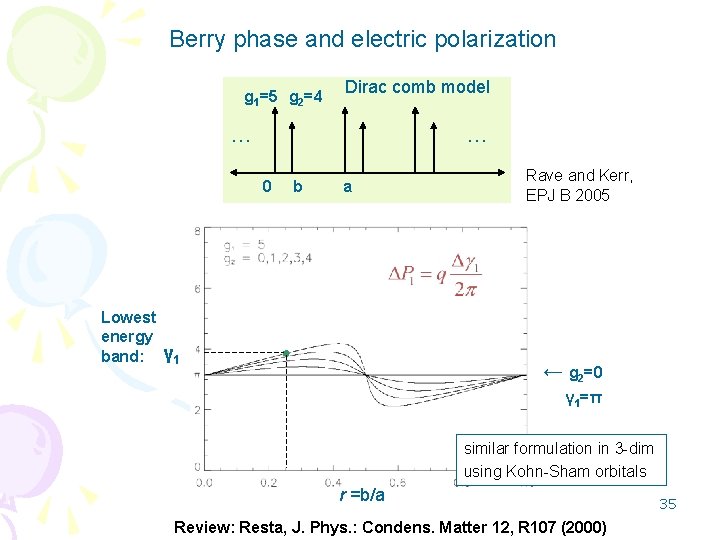
a concept is introduced for physical equivalence of energy bands in solids two energy bands are physically equivalent if their branches have identical continuity chords (symmetries) and identical berry phases 14 pairs of simple bands exist that are described by equivalent band representations but are nevertheless physically inequivalent because Over the past three decades it was gradually realized that the Berry phase of the electronic wave function can have a profound effect on material properties and is responsible for a spectrum of phenomena, such as polarization, orbital magnetism, various (quantum, anomalous, or spin) Hall effects, and quantum charge pumpingGuage invariance and electron dynamics in solids, Berry's phase correction to electron dynamics, Berry's curvature Handout 16 Inversion symmetry of energy bands, current density in energy bands, electronhole transformation, conductivity of electrons in conduction bands and holes in valence bands, conductivity tensor of semiconductors
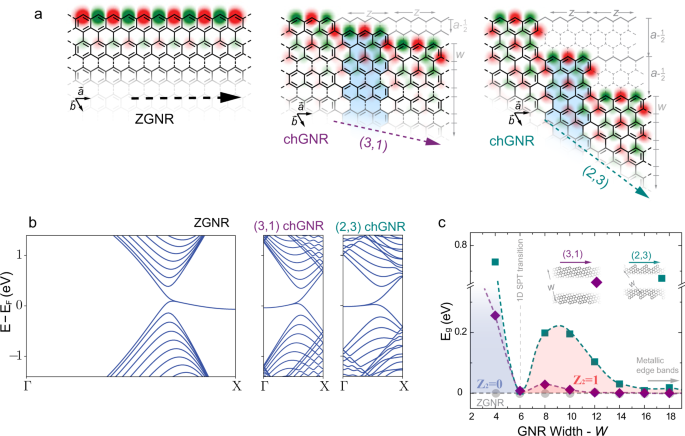



Topological Phase Transition In Chiral Graphene Nanoribbons From Edge Bands To End States Nature Communications



Bourbaphy Fr
(2 atoms/uc) BZ is halffilled #electrons in the reciprocal unit cell from the UvA VU Master Course Advanced Solid StateBerry phase Consider a closeddirected curve C in parameter space R The Berryphase along C is defined in the following way X i ∆γ i → γ = −Arg exp −i I C A(R)dR Important The Berry phase is gaugeinvariant the integral of ∇ Rα(R) depends only on the start and end points of C, hence for a closed curve it is zero November 17Including the dynamical phase) may not return to its original value after a cyclic evolution in parameter space This fact was first exposed clearly by Micha el Berry 3 in his 1984 paper In this section, we introduce the basic concept of the Berry phase, in later sections we will move on to examples of the Berry phase in condensed matter




Electronic Band Structure Wikipedia




Band Structures Of The Kane Mele Model In The Normal Phase Top And Download Scientific Diagram
The Berry phase in a two band theory is given by half the solid angle swept out by ˆ d(k) (7) γC = 1 2(Solid angle swept out by ˆ d(k)) In particular, when C corresponds to a 2π rotation of ˆ d in a plane, the Berry phase is πBerry's Phase for Energy Bands in Solids 3 Zak Department ofPhysics, Technion Israel Institute of TechnologyH, aifa 300, Israel (Received 28 December 19) Berry's phase is defined for the dynamics of electrons in periodic solids and an explicit formula is derived for it Because of the special torus topology of the Brillouin zone aIn this thesis, I will present and discuss the results of three experiments where Berry's phase leads to qualitatively new transport behavior of electrons or magnetic spin excitations in solids We introduce the theoretical framework that leads to the prediction of a thermal Hall effect of magnons in Cu(1,3bdc), a simple twodimensional



1
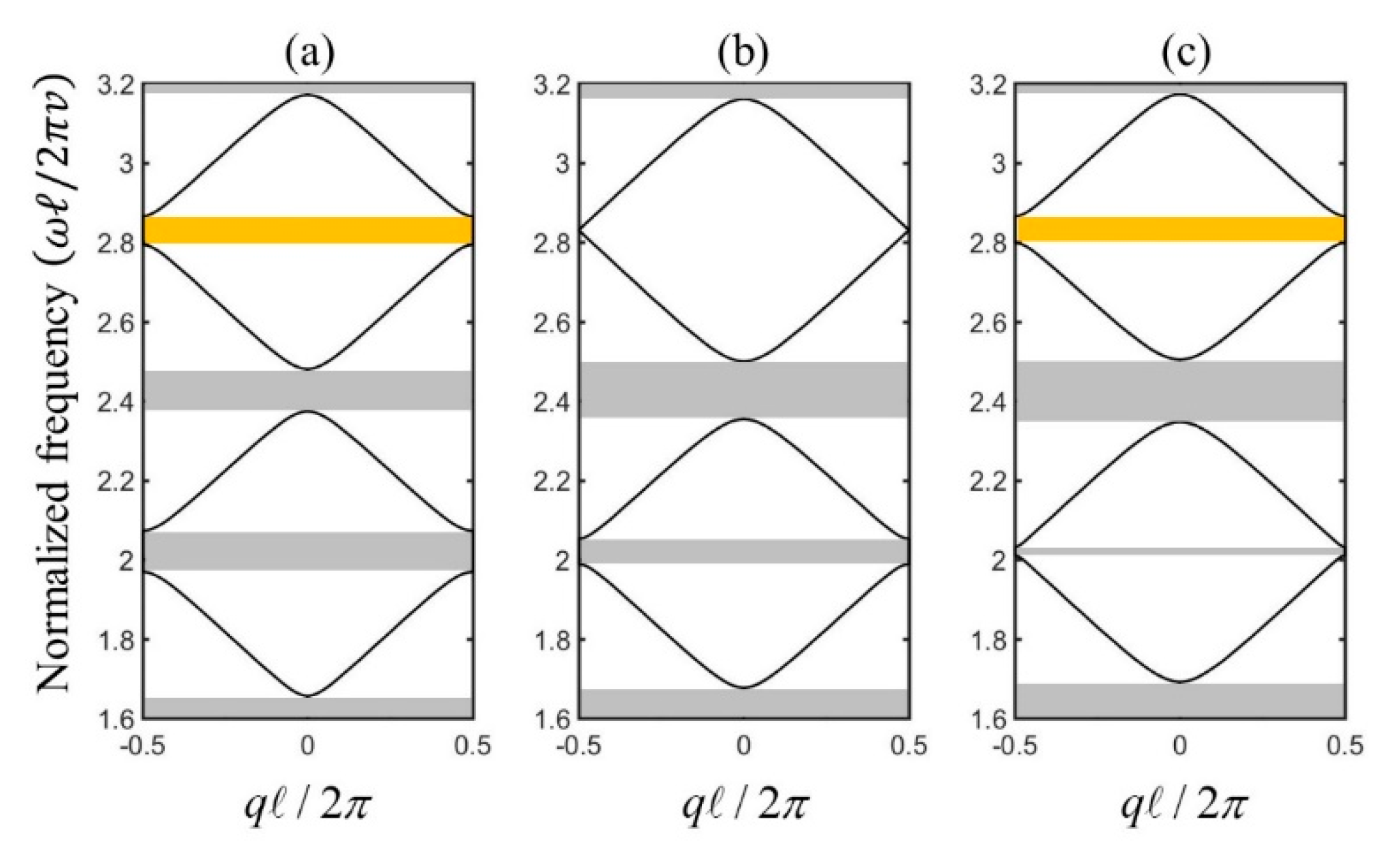



Crystals Free Full Text Topological Phase Transition In A One Dimensional Elastic String System Html
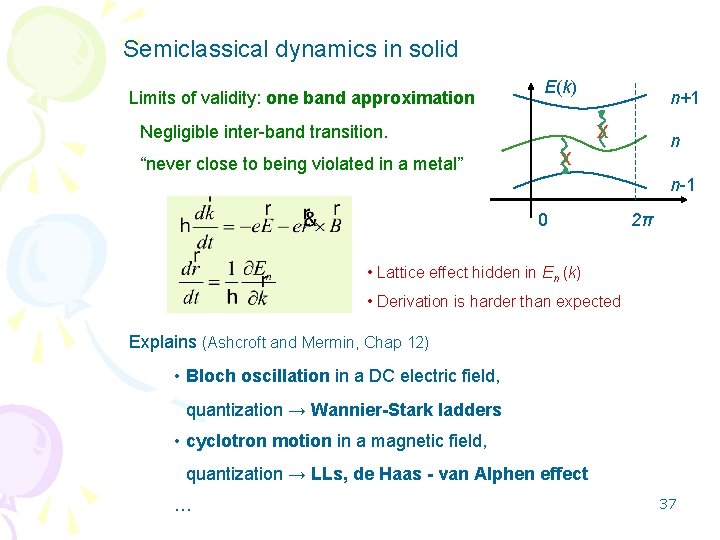
• The behavior of electrons in energy bands subjected to uniform electric fields • The dynamical equation for the crystal momentum • The effective mass tensor and inertia of electrons in energy bands • Examples • Magnetic fields • Appendix Electron dynamics using gauge invariance arguments, Berry's phase, and Berry's curvature Hi, All In searching for images related to the introduction of band theory in solid sate physics I found this one I would like to ask you if I am correct in thinking the increase in the number of splittings (in b) is misleading to students Thank you all Best regards, DaTario The topological properties of 1D solids are characterized by the socalled Zak phase—the Berry's phase picked up by a particle moving across the Brillouin zone 12 For a given Bloch wave ψk ( x)
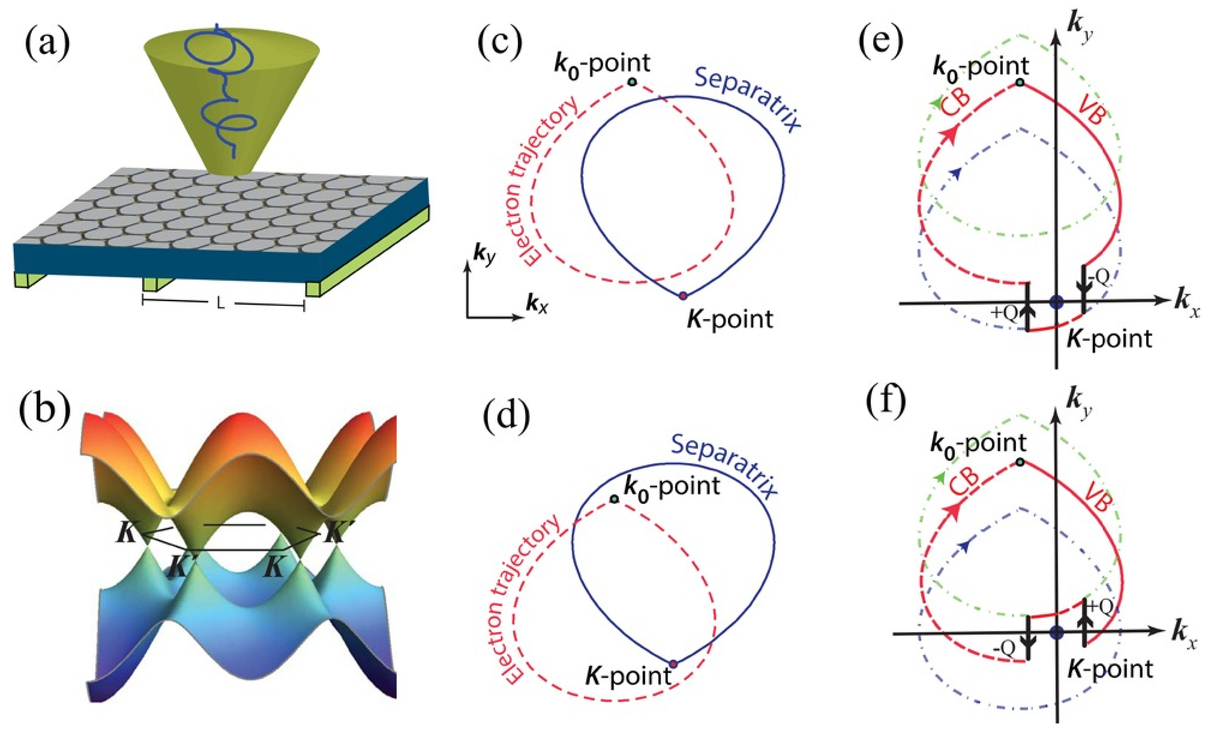



How To Detect Berry Phase In Graphene Without Magnetic Field




Berry Phase Effects On Electrons Qian Niu University



Topological Edge States Controlled By Next Nearest Neighbor Coupling And Peierls Phase In A P T Symmetric Trimerized Lattice




Berry S Phase Youtube



Topologically Protected Plasmon Mode With Ultrastrong Field Localization In A Graphene Based Metasurface



1




Measuring The Berry Phase Of Graphene From Wavefront Dislocations In Friedel Oscillations Nature



Energy Band Structures In Solids Technical Articles




Band Theory Of Solids Notes




A Review On Energy Band Gap Engineering For Perovskite Photovoltaics Hu 19 Solar Rrl Wiley Online Library
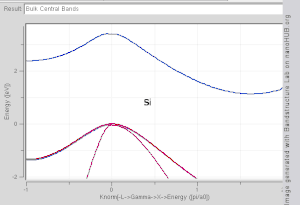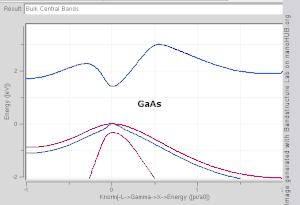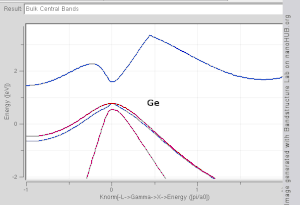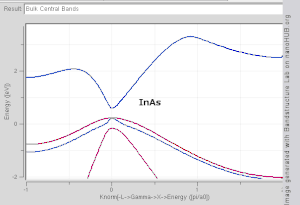



Electronic Band Structure Wikipedia
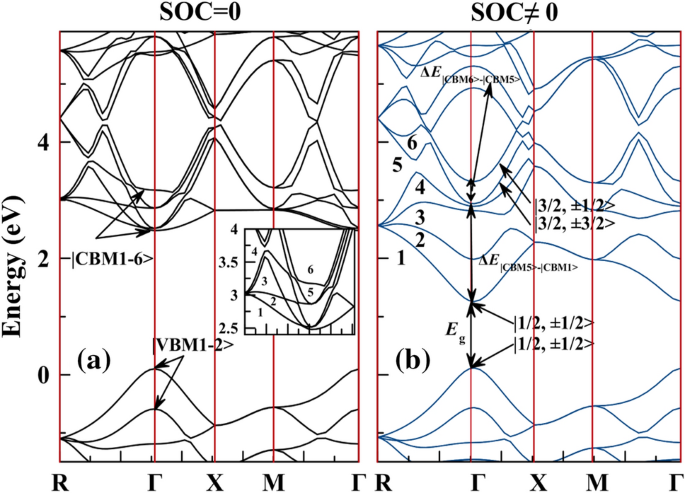



Spin Orbit Coupling Effect On Energy Level Splitting And Band Structure Inversion In Cspbbr3 Springerlink




Berry Phase Effects On Electrons Ppt Video Online Download



Bourbaphy Fr
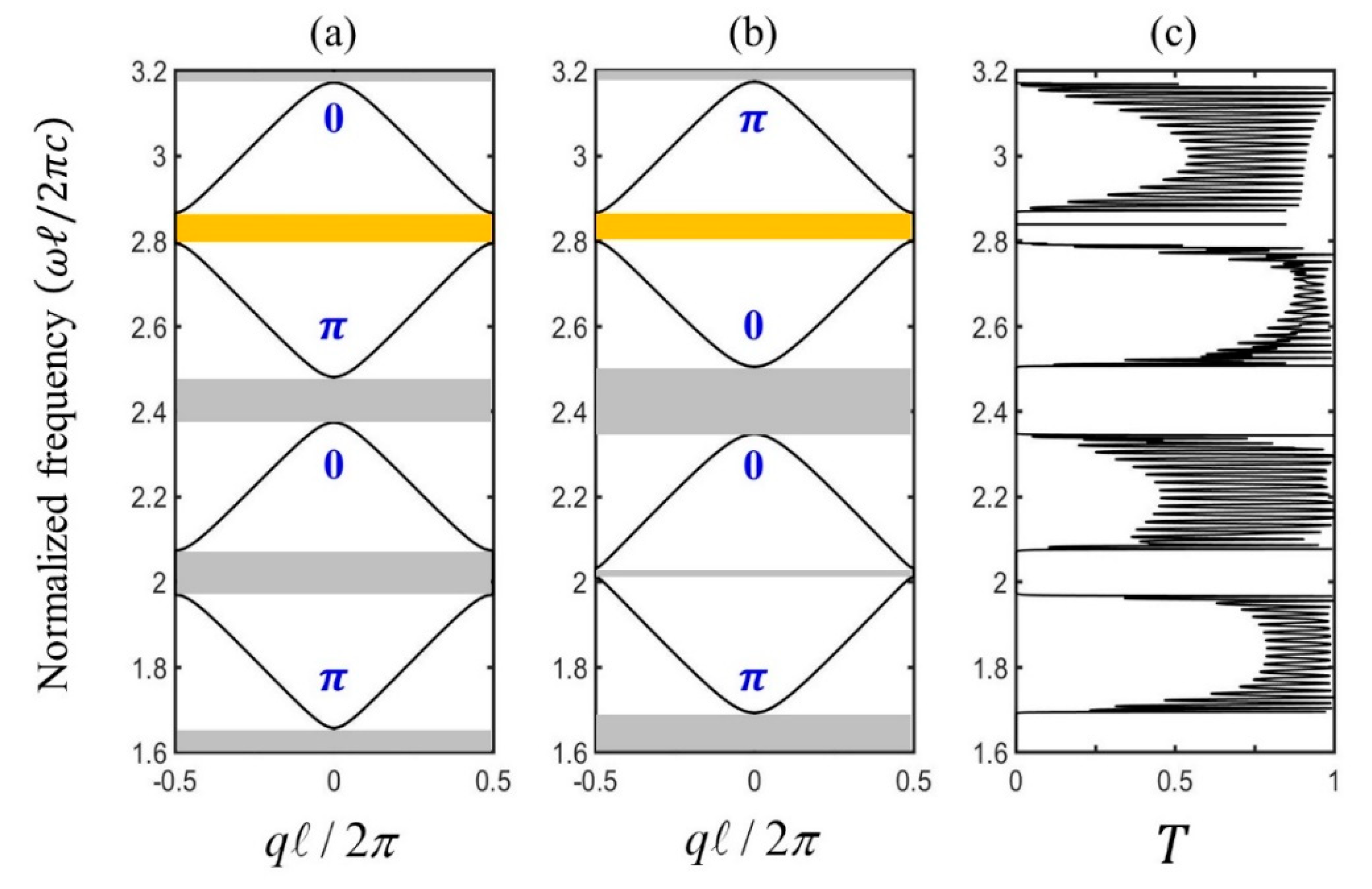



Crystals Free Full Text Topological Phase Transition In A One Dimensional Elastic String System Html



Band Theory In Solids Origin Of Energy Bands Formation In Solids An Isolated Atom Possesses Discrete Energies Of Different Electrons Suppose Two Isolated Atoms Are Brought To Very Close Proximity Then The Electrons In The Orbits Of Two Atoms Interact With



Influence Of A Site Cation On Nonlinear Band Gap Dependence Of 2d Ruddlesden Popper pb1 Xsnxi4 Perovskites Materials Advances Rsc Publishing



Energy Band Structures In Solids Technical Articles




Nonadiabatic Berry Phase In Nanocrystalline Magnets Aip Advances Vol 7 No 5




12 Phy 17 Energy Bands In Solids On Vimeo



Topological Edge States Controlled By Next Nearest Neighbor Coupling And Peierls Phase In A P T Symmetric Trimerized Lattice



The Berry Phase And The Quantum Hall Effect Book Chapter Iopscience




Berry Curvature And Circular Dichroism In Hbn A Berry Curvature V Download Scientific Diagram
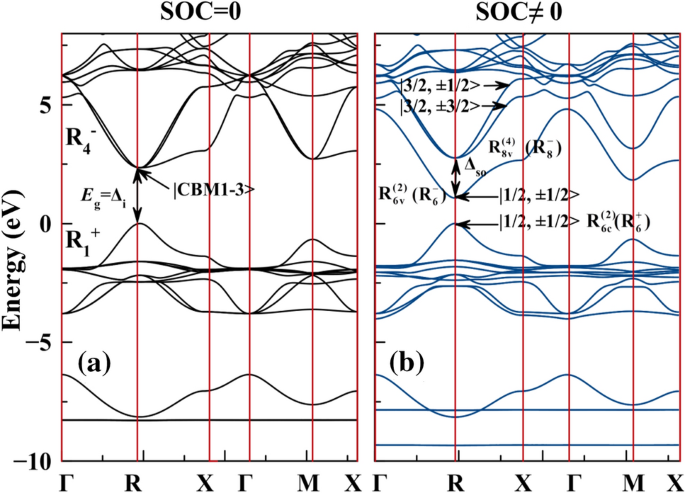



Spin Orbit Coupling Effect On Energy Level Splitting And Band Structure Inversion In Cspbbr3 Springerlink



Band Theory In Solids Engineering Physics Class
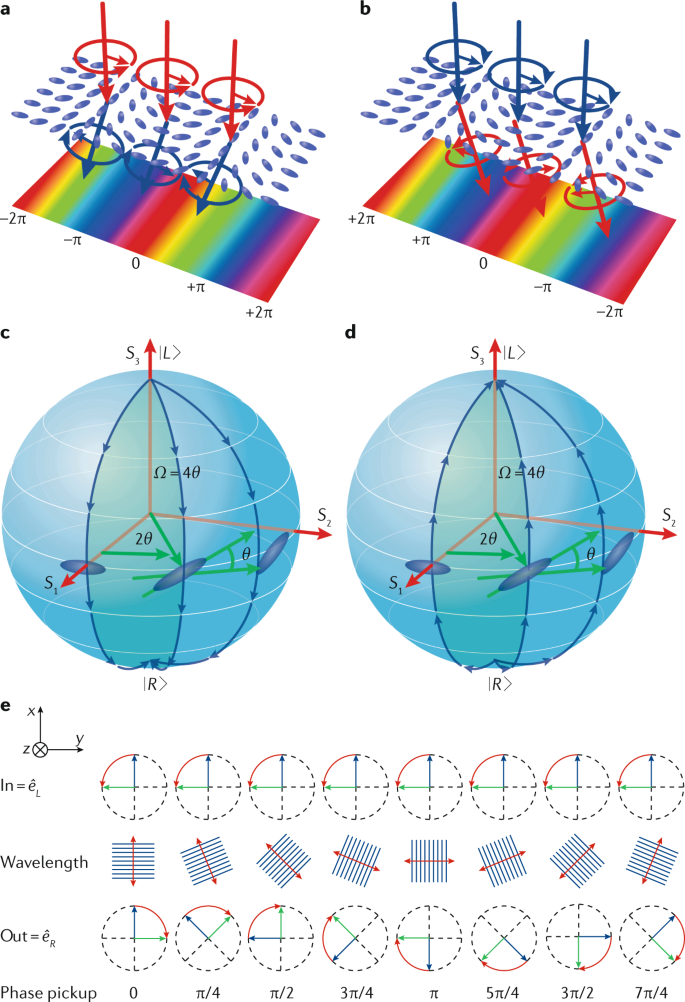



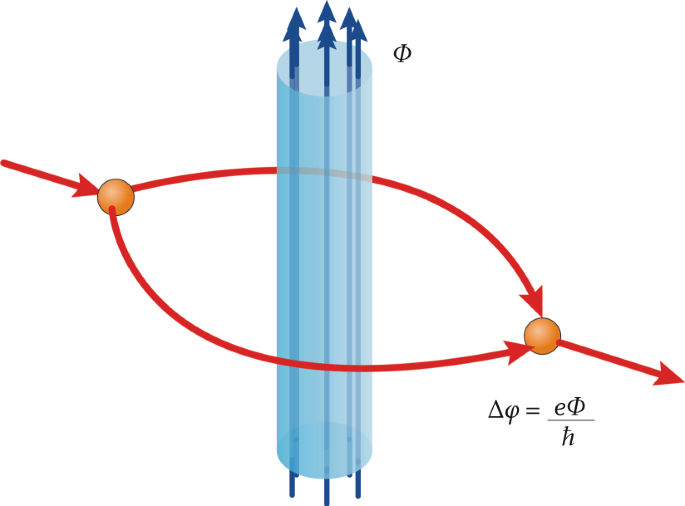
Geometric Phase From Aharonov Bohm To Pancharatnam Berry And Beyond Nature Reviews Physics



Juelich Berry Phase In Solid State Physics




Juelich Berry Phase In Solid State Physics




Berry Phases In Electronic Structure Theory



Link Aps Org




First Principle Study Of Band Gap Nature Spontaneous Polarization Hyperfine Field And Electric Field Gradient Of Desirable Multiferroic Bismuth Ferrite Bifeo3 Sciencedirect




Berry Phase In Solid State Physics Ppt Video Online Download



Juelich Berry Phase In Solid State Physics



Refubium Fu Berlin De



Arxiv Org



Hal Archives Ouvertes Fr



Energy Bands In Solids And Their Calculations Mse 5317




The Band Gap Solid Line And The Pancharatnam Berry Phase Dashed Of Download Scientific Diagram




Nonadiabatic Berry Phase In Nanocrystalline Magnets Aip Advances Vol 7 No 5




Unraveling Materials Berry Curvature And Chern Numbers From Real Time Evolution Of Bloch States Pnas



Geometric Phase From Aharonov Bohm To Pancharatnam Berry And Beyond Nature Reviews Physics




Unraveling Materials Berry Curvature And Chern Numbers From Real Time Evolution Of Bloch States Pnas




Nodal Line Band Crossing And Its Large Berry Curvature In Fe3gete2 A Download Scientific Diagram



Iht Univ Kiev Ua
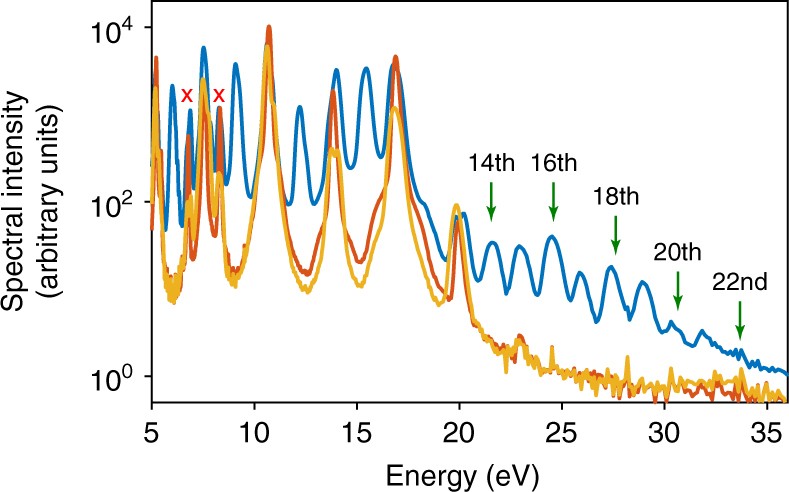



Measurement Of The Berry Curvature Of Solids Using High Harmonic Spectroscopy Nature Communications




Nodal Line Band Crossing And Its Large Berry Curvature In Fe3gete2 A Download Scientific Diagram
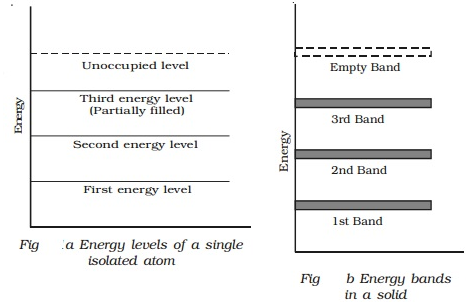



Energy Band In Solids




Pressure Induced Nodal Line Semimetal In Yh3



Iht Univ Kiev Ua
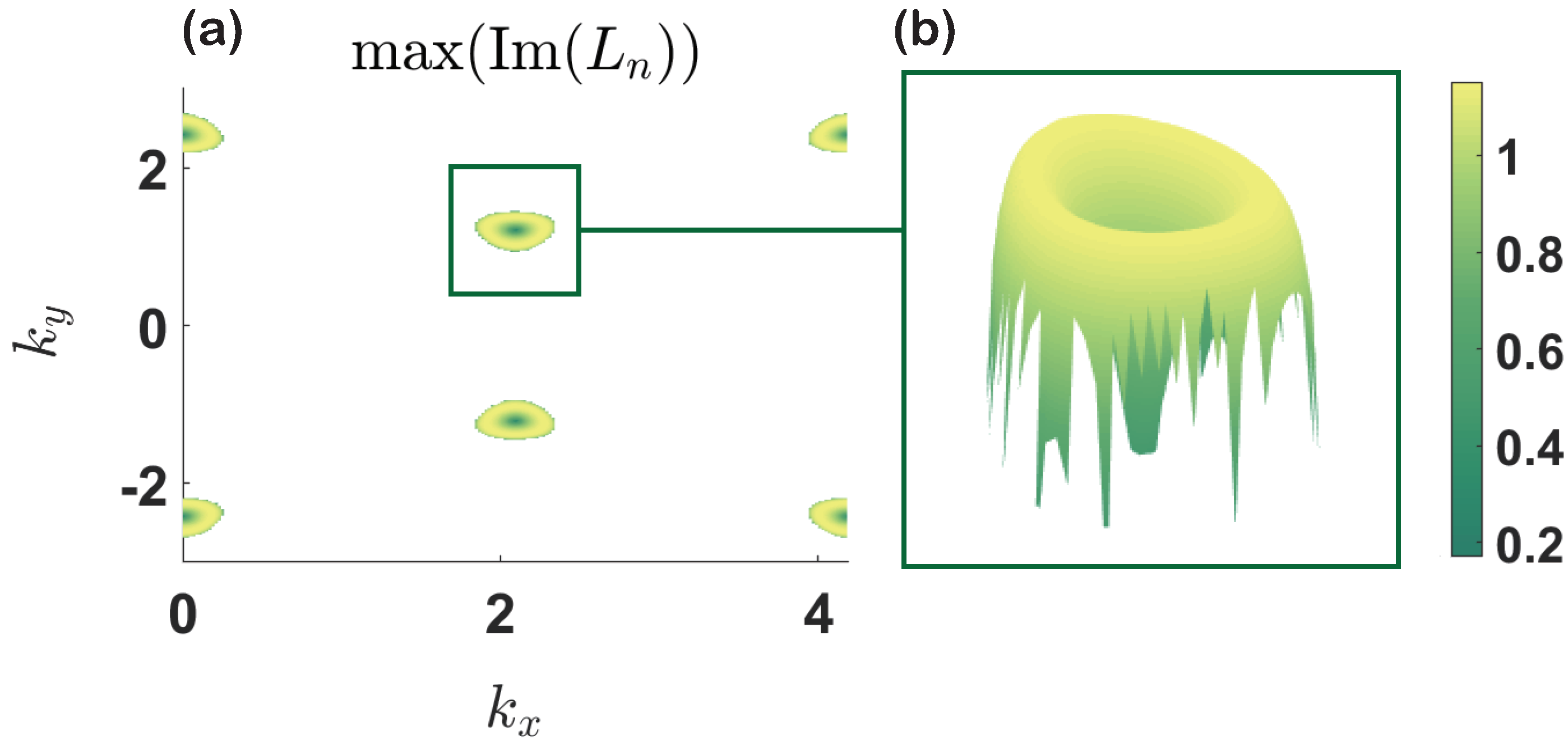



Entropy Free Full Text Nonlinear Topological Effects In Optical Coupled Hexagonal Lattice Html




The Berry Phase In Graphene And Graphite Multilayers Low Temperature Physics Vol 34 No 10




Quadrupole Topological Photonic Crystals Journal Article Doe Pages




Berry Phase Effects On Electronic Properties Ppt Video Online Download
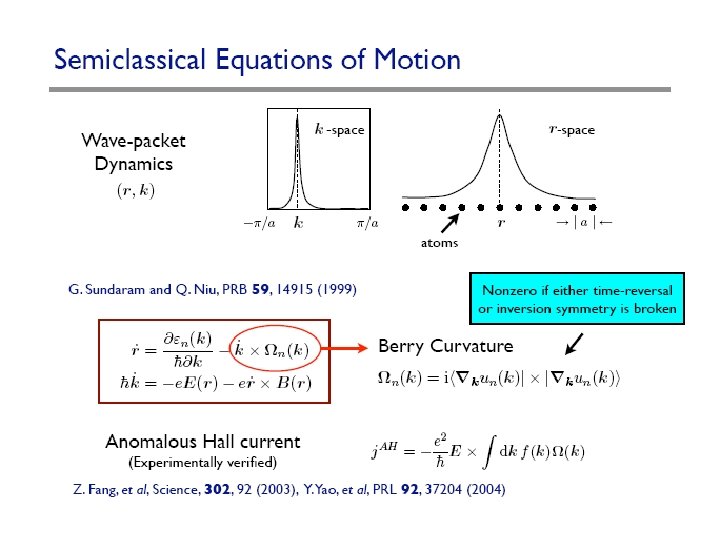



Berry Phase Effects On Electrons Qian Niu University



Ens Lyon Fr
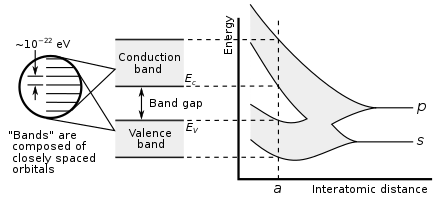



Electronic Band Structure Wikipedia



Tight Binding Github Topics Github



D Nb Info



The Berry Phase And The Quantum Hall Effect Book Chapter Iopscience
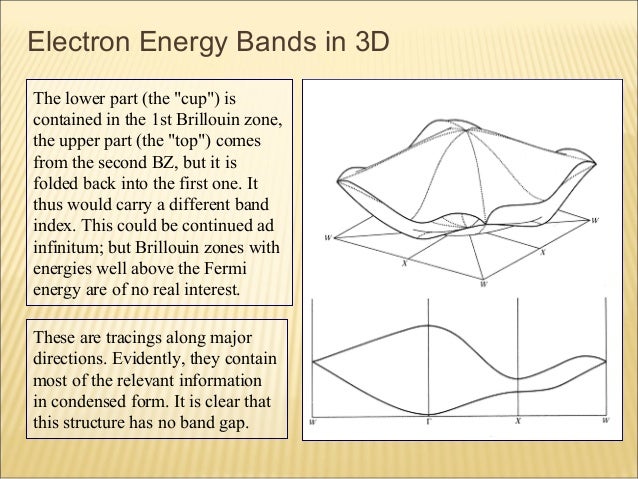



Energy Band Theory Of Solids
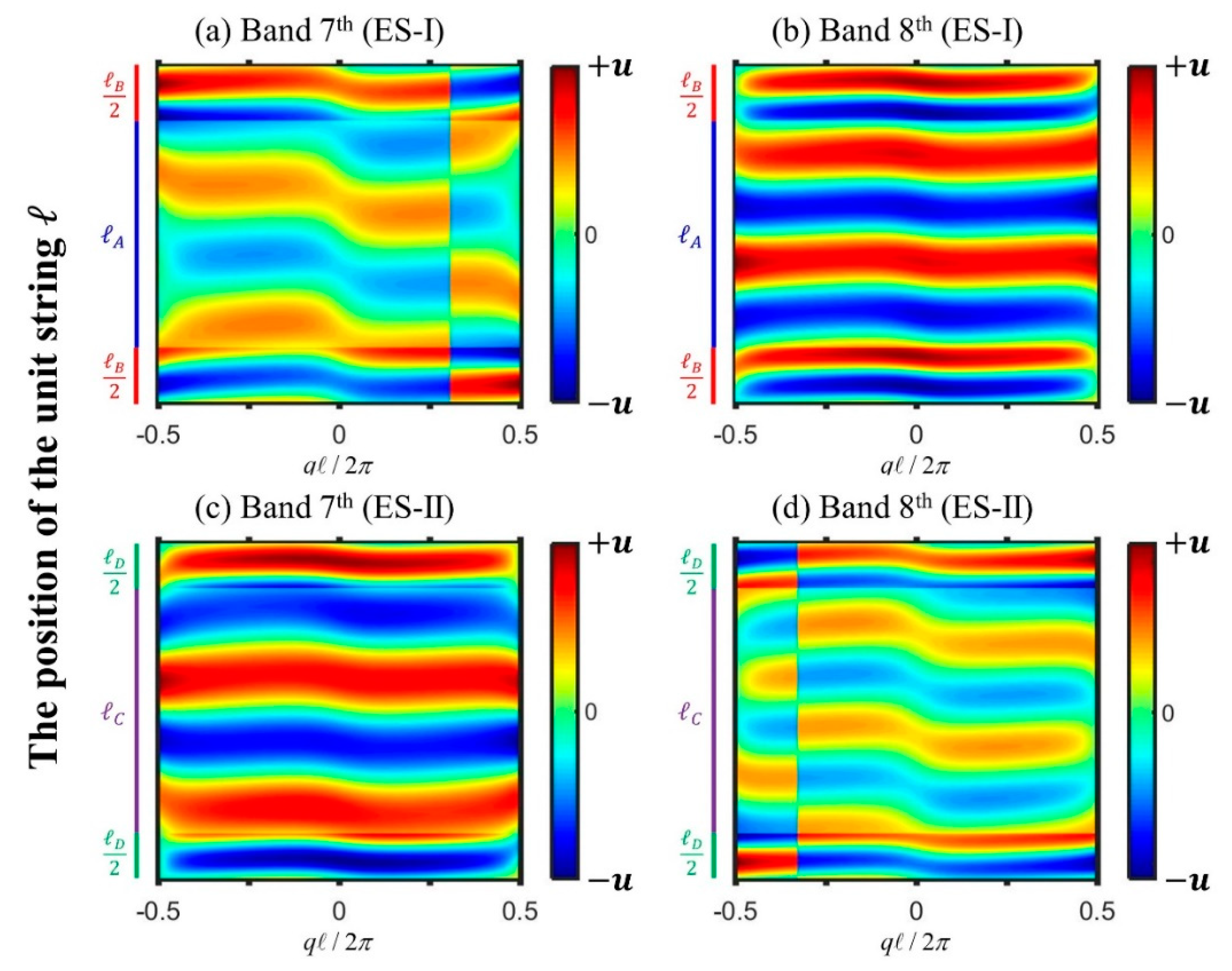



Crystals Free Full Text Topological Phase Transition In A One Dimensional Elastic String System Html




Berry Phase In Solid State Physics Ppt Video Online Download



1




Band Theory Of Solids Notes



D Nb Info




Phys Rev X 8 18 Inequivalent Berry Phases For The Bulk Polarization
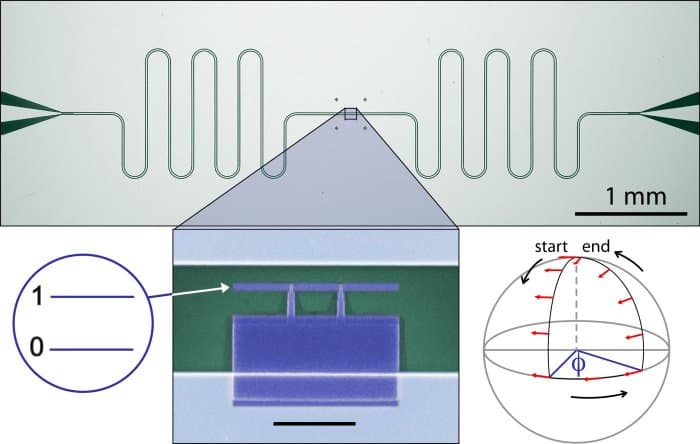



Berry S Phase Seen In Solid State Qubit Physics World




Ppt Energy Bands In Solids Powerpoint Presentation Free Download Id



Wwwphy Princeton Edu
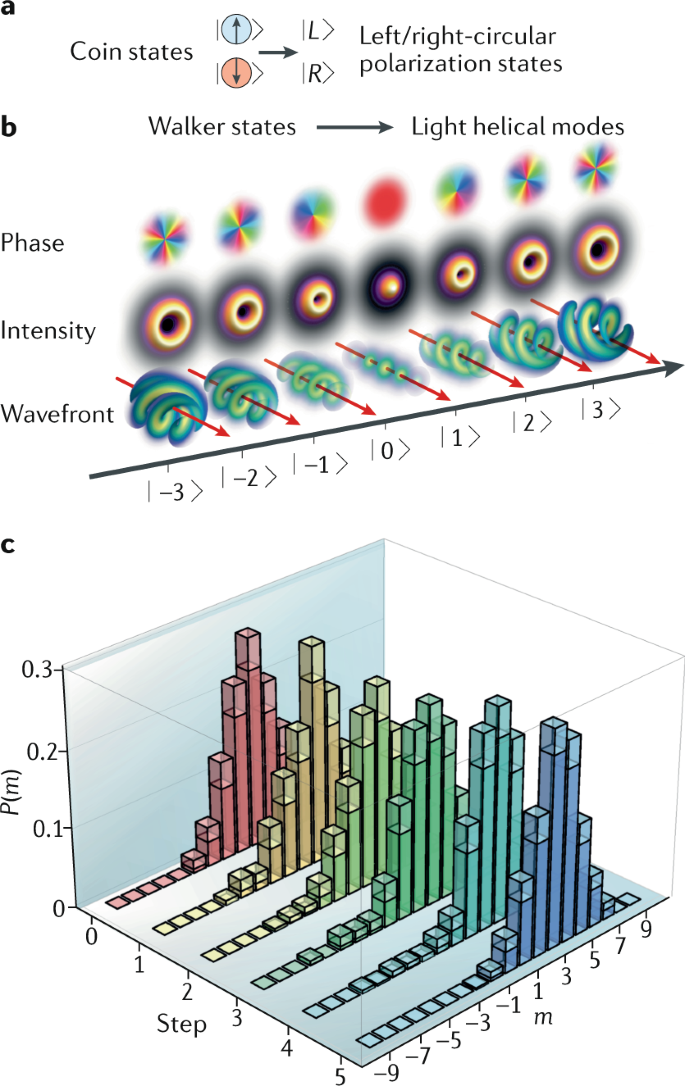



Geometric Phase From Aharonov Bohm To Pancharatnam Berry And Beyond Nature Reviews Physics



Arxiv




Berry Phase An Overview Sciencedirect Topics




Berry Phase Effects On Electrons Qian Niu University



1




Berry Phase Effects On Electrons Qian Niu University




Unraveling Materials Berry Curvature And Chern Numbers From Real Time Evolution Of Bloch States Pnas




Evidence Of Both Surface And Bulk Dirac Bands And Anisotropic Nonsaturating Magnetoresistance In Zrsis Wang 16 Advanced Electronic Materials Wiley Online Library



Physics Iisc Ac In




Pdf Berry Phase And Band Structure Analysis Of The Weyl Semimetal Nbp




Effect Of Spin Berry Phase A The Spin Berry Phase Wijk Is Equal To Download Scientific Diagram
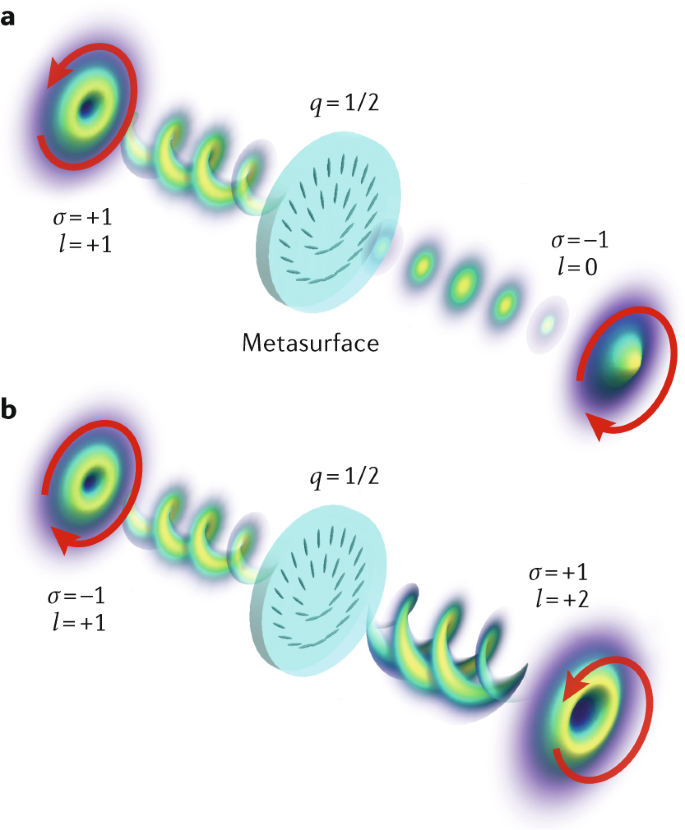



Geometric Phase From Aharonov Bohm To Pancharatnam Berry And Beyond Nature Reviews Physics



Electronic Band Structure Wikipedia



0 件のコメント:
コメントを投稿