Continue this process decrementing the power of x and incrementing the power of y until you place the term y n next to the final number 1x 5 5 x 4 y 10x 3 y 2 10x 2 y 3 5xy 4 1y 5 Exercises Expand (2x y) 4 (x y) 6(xyz)^3 (x y z)(x y z)(x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy y * y = y^2 (xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions "This can be done by expanding out the brackets, but there is a more elegant solution" Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agree
Modular Xyz Xpansion Pins Mitee Bite Products Llc
What is the formula of (x+y+z)^3
What is the formula of (x+y+z)^3-Solutions Manual Business Accounting; Find an answer to your question 3 Expand (i) (x y z)^2 akshayagkg00gmailcom is waiting for your help Add your answer and earn points




3 Expand I X Y Z 2
0 0 Similar questions Factorise and simplify 6 4 x 1 2 − 5 1 2 Medium View solution > Factorise 6 4 m 3 − 3 4 2 n 3 Medium View solution > If (y x x y = − 1) (x, y = 0), the value of (x 3 − y 3) is, Medium View solution > If a = 4965, b = 2343 and c = 2622, then (a 3Rewrite (x−y −z)2 ( x y z) 2 as (x−y−z)(x−y−z) ( x y z) ( x y z) Expand (x−y−z)(x−y−z) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x x Step 1 The given logarithm expression can be expanded using following properties of logarithms The exponent property is log a x y = y log a x The sum property of logarithms is log a x log a y = log a x y The difference property of logarithms is log a x − log a y = log a x y Step 2 The given expression is log 3 3 x 5 y
Expand (x^2y^2z^2)^3(xyz)^3*x*y*z Natural Language; Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the other terms in the other brackets, but never multiply two or Use the Laws of Logarithms to expand the expression a \(\displaystyle{\log{{\left({\left\lbrace{\frac{{{x}{y}^{{3}}}}{{{z}^{{2}}}}}\right\rbrace}\right)}}}\)
Expand (x y z)^10 Natural Language; if x^2y^2z^2=xyyzzx then find the value of x^3y^3z^3 We will work with the RHS part here, (x y z) ( x² y² z² xy yz zx) Expanding the entire bracket, = x³ xy² xz² x²y xyz zx² yx y³ yz² xy² y²z xyz zx² zy² z³ xyz yz² z²x =x³Example Express the Boolean function F = x y z as a sum of minterms Solution F = x y z = x (y z) AND (multiply) has a higher precedence than OR (add) = x(yy')(zz') (xx')yz expand 1st term by ANDing it with (y y')(z z'), and 2nd term with (x x') = x y z x y z' x y' z x y' z' x y z x' y z = m7 m6 m5 m4 m3



Help Online Tutorials Basic 3d Plotting




Expand X Y Z 2 X Y Z 2 Brainly In
Using x = 2, y = 3, and z = 4, evaluate each expression and match to its corresponding answer SW 1 ху 2 A) 6 2 х(у 2) B) 1 3 2z Зу C) 2 4 x yz D) 14 5 ху— хz E) 12 6 2(г— х) F) 1 7 yz X y G) x y 8 X z Н) 2 9 2(х у) I) 4 10 ху yz J) 14 fullscreen Expand check_circle Expert Answer Want to see the stepbystep answer?Use the following identity which also gives you the exact deviation in positive terms from $27 x y z$ (from which you can derive tighter bounds of the LHS) $$ (xyz)^3 = 27 x y z 3 (zy)^2 x 3 (xz)^2 y 3 (yx)^2 z \\ \frac12 (xyz)((xy)^2 (yz)^2 (zx)^2) $$ All terms on the RHS are positive, so you can take lower bounds of the LHS by any term on the RHS or weighted sum (xy)^4 = x^4y^4z^44x^3y4xy^34y^3z4yz^34z^3x4zx^36x^2y^26y^2z^26z^2x^212x^2yz12xy^2z12xyz^2 Note that (ab)^4 = a^44a^3b6a^2b^24ab^3b^4 So we can find the terms of (xyz)^4 that only involve 2 of x, y, z by combining the expansions of binomial powers, One way to see that is



2



Videos Expand The Expression X Y Z 2 Snapxam
The Baker–Campbell–Hausdorff formula supplies the necessary correction terms Transcendency The function e z is not in C(z) (that is, is not the quotient of two polynomials with complex coefficients) For n distinct complex numbers {a 1, , a n}, the set {e a 1 z, , e a n z} isExpand Evaluate Fractions Linear Equations Quadratic Equations Inequalities Systems of Equations Matrices Trigonometry Simplify Evaluate Graphs Solve Equations Calculus Derivatives Integrals Limits Algebra Calculator Trigonometry Calculator Calculus Calculator Matrix Calculator Solve algebra trigonometry statistics calculus matrices variables list Solve forIn elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive



Logarithms Expanding Log Expressions 1 4 Youtube



Ihcru3ob06yakm
Expand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions onlineFree expand & simplify calculator Expand and simplify equations stepbystep This website uses cookies to ensure you get the best experience By using thisClick here👆to get an answer to your question ️ Expand ( 2x 5y 3z )^2 using suitable identities Join / Login >> Class 9 >> Maths >> Polynomials >> Algebraic Identities >> Expand ( 2x 5y 3z )^ Question Expand (− 2 x 5 y − 3 z) 2 using suitable identities Hard Open in App Solution Verified by Toppr (− 2 x 5 y − 3 z) 2 is of the form (a b c) 2 (a b c




42nd Edition Abc Xyz Of Bee Culture




Nonplanar Xyz Provides The Tools To Use The Z Axis Correctly In Fdm Printing 3dnatives
Answer to How to expand x^3y^3? For this question, you can use the Multinomial Theorem (a version of the Binomial Theorem for three or more terms) Or, you can group the terms (as in, ((xy) z) n) and apply the Binomial Theorem as usualSupport@crazyforstudycom 1 (775) ;
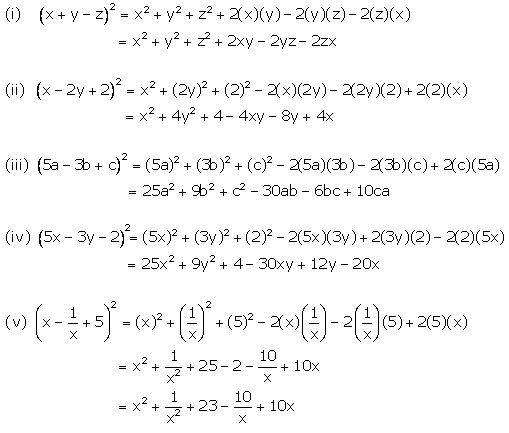



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning




Genmitsu Cnc Router Machine Proverxl 4030 Xyz Working Area 400 X 300 X 110mm 15 7 X11 8 X4 3 Proverxl 4030 Xy Axis Extension Kit Upgraded Accessories Expand From 4030 To 6060 24 X 24 Amazon Com
Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3Extended Keyboard Examples Upload Random Examples Upload RandomGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



63 Write The Expression As A Single Logarithm Gauthmath




X Y 2 3 Find The Expansion Of The Following Brainly In
See Answer Check out aStepbystep Solution Expand the logarithmic expression $\log \left(\sqrt3{\frac{\left(x5\right)^4}{x^2}}\right)$Imagine I have a 3 columns matrix x, y, z where z is a function of x and y I know how to plot a "scatter plot" of these points with plot3d(x,y,z) But if I want a surface instead I must use other commands such as surface3d The problem is that it doesn't accept the same inputs as plot3d it seems to need a matrix with



Answered O Expanding A Logarithmic Expression In Bartleby




Triangle Xyz Is Reflected About The Y Axis What Are The Coordinates Of X Brainly Com
The other way of seeing "term" is just simply as the amount of combinations you can take out of $(xyz)^n$ which would result into $3^n$ Depending on what is the right interpretation, how can I provide proof for it?Tìm x,y,z biết 3x5 (2 y 5) 8 (4 z3) ≤ 0 Trả Lời Hỏi chi tiết Trả lời trong APP VIETJACKXem câu hỏi chi tiết Quảng cáo 3 câu trả lời 259 Đoàn Thị Xuân 2 tháng trước X 0 bình luận 1 (50 ) Đăng nhập để hỏi chi tiết Hoàng Thị Hiên 2 tháng trước t a c ó 3 x5 ≥ 0 v ớ i m ọ i x ∈ R 2 y 5 8Answer (1 of 5) First of all, we observe the following formula {{\left( a\,\,b \right)}^{\,3}}\,=\,{{a}^{\,3}}\,\,{{b}^{\,3}}\,\,3\,a\,b\,\left( a\,\,b \right



Camschat Xyz Urlscan Io



Bestlolivds Xyz Urlscan Io
Expand ( X Y Z )2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Expand ( X Y Z )2 MathematicsThe identity exp(x y) = exp x exp y can fail for Lie algebra elements x and y that do not commute;Here's a straightforward way, which is not very elegant, but is on the other hand very general, and does not require problemspecific tricks We want to calculate bounds for the function f=x y



Startup Pitch To Raise Capital From Crowdfunding Geographic Expansion Strategy Topics Pdf Powerpoint Templates



1
WolframAlpha Computational Intelligence Natural Language Math Input NEW Use textbook math notation to enter your math Try it × Extended Keyboard Examples Compute expertlevel answers using Wolfram's breakthrough algorithms, knowledgebase and AI technologyExpand (− 2 x 5 y − 3 z) 2 using suitable identities Mathematics Q5 Expand the following, using suitable identities 1) − 2 x 3 y 2 z) 2 2) (− 2 x 5 y − 3 z) 2 4 MARKS Mathematics NCERT Exemplar Standard VIII Q1 Question 85 (x) Expand the following, using suitable identities (2 x − 5 y) (2 x − 5 y) Mathematics RS Agarwal Standard IX Q2 Expand each of the`log_(3)x 2log_(3)y3log_(x)z` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERT Fingertips Errorless Vol1 Errorless Vol2 Maths NCERT RD Sharma Cengage KC Sinha Download PDF's Class 12 Class 11 Class 10 Class 9 Class 8 Class




Solved Condense 3 Log X 4 Log Y Log X 3 Y 4 Log Chegg Com




Xyz Leadership
Solved Expert Answer to A By starting with ( (x y) z) 3, expand (x y z) 3 b Find the term independent of x in the expansion of (x 1 x ?1) 4 Get Best Price Guarantee 30% Extra Discount;Expand each single logarithm as much as possible {eq}a log_a (xy)^4/3\\ b log_3 (z/5)^{2x}\\ c log_5 \sqrt7{x^3}\\ d log_8 \frac{\sqrt{x}y^7}{z^5}Hence, (x − y) 3 (y − z) 3 (z − x) 3 = 3 (x − y) (y − z) (z − x) Was this answer helpful?




Lcm Of S Monomials Binomials Student Reference 3 Assignments For Smart




X Y Y Z Z X 2 Write It In The Expanded Form Brainly In
Algebraprecalculus binomialcoefficients Share Cite Follow edited Oct 30 '11 at 1258 Martin Sleziak 507k 18 18 gold badges 162 162 silver badges 327 327 bronzeSection 35 Minterms, Maxterms, & Canonical Forms Page 2 of 4 A maxterm, denoted as Mi, where 0 ≤ i < 2n, is a sum (OR) of the n variables (literals) in which each variable is complemented ifמחשבון הרחבה ופישוט הרחב ופשט ביטויים אלגברים צעד אחר צעד



1 Expand Each Logarithm A Log 2 5 X B Log Gauthmath




3d Tiskarna Xyz Da Vinci Mini W Cerna Pla Petg Tough Pla Antibacte Pla 15x15x15 Cm 100 400 Mikronu Usb 2 0 Wi Fi Ed System A S
(xyz)2 expand the xyz) 2541If x y z = 6 and x 2 y 2 z 2 = then the value of x 3 y 3 z 3 – 3xyz is Please scroll down to see the correct answer and solution guideIn this maths class, we will learn about expansion from class 9's algebra section Which will include1 identity viii x^3y^3z^33xyz=(xyz)(x^2y^2z^2
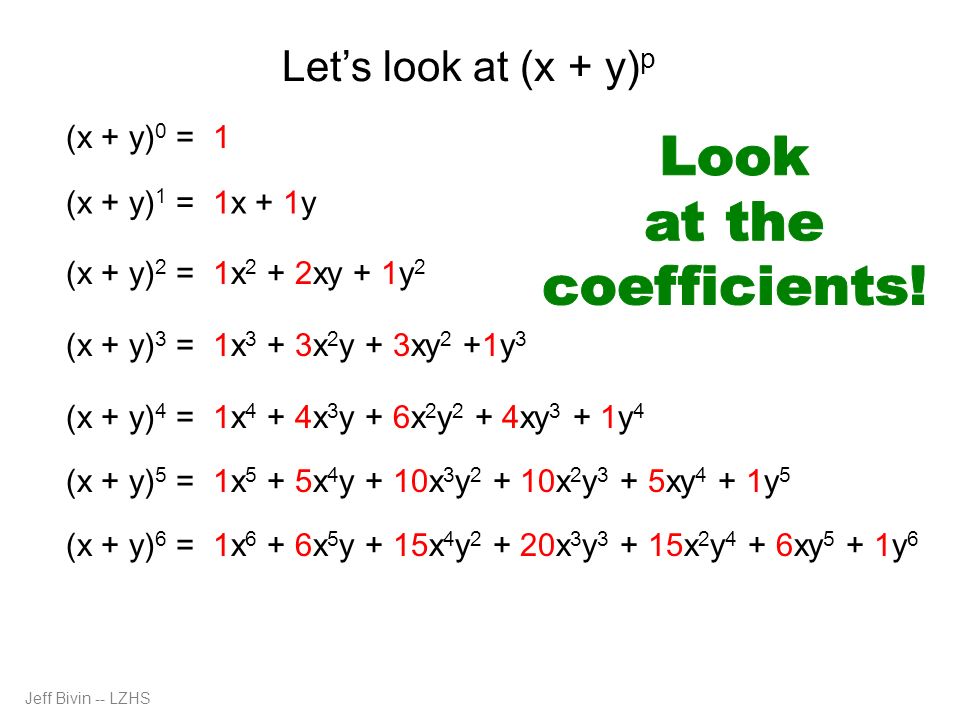



Binomial Expansion And More Ppt Download
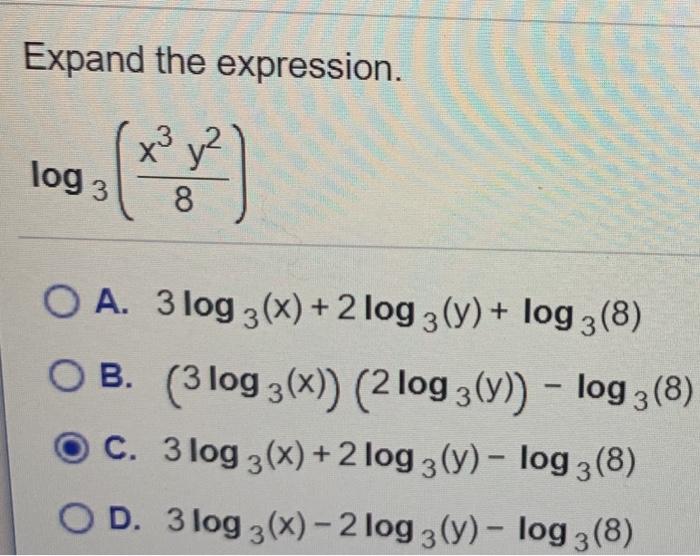



Solved Expand The Expression X Y Z Log3 8 O A 3 Log 3 X Chegg Com
You can put this solution on YOUR website!Arrange the expression in the form of factorization (x y z)(xy yz zx)− xyz ( x y z) ( x y y z z x) − x y z Expand the expression x2y x2z xy2 2xyz xz2 y2z yz2 x 2 y x 2 z x y 2 2 x y z x z 2 y 2 z y z 2 Do factorization (x y)(x z)(y z) ( x y) ( x z) ( y z) x^3y^3z^3=42 L'équation diophantienne faisant office de titre de ce billet fut posée en 1954 à l'université de Cambridge La question était de trouver, pour tous les nombres entiers entre 1 et 100, les valeurs de x, y et z Les cas faciles furent vite évacués, restèrent pendant des décennies les deux cas les plus compliqués 33




Xyz File Format Semantic Scholar




Xyz Affair Wikipedia
Insert x n1 y next to the second number of Pascal's Triangle and add a "" sign 1x 5 5 x 4 y 10 10 5 1 ;By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask yourExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel




Modular Xyz Xpansion Pins Mitee Bite Products Llc




Ppt Binomial Expansion And More Powerpoint Presentation Free Download Id



Solved Can T Move Vip Fortunatepeople Xyz Malware Malwaretips Community




Math 1111 Unit 4 Test 4 Properties Of Logarithms Youtube



1



Geller Magnification Calibration Standard Mrs 4xyz Calibrated In Xyz But Without Retainer Ring Ab Spi Supplies



1



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University




Top 10 Strongest Rank 10 Xyz Monsters In Yu Gi Oh Hobbylark




In The Expansion Of X Y Z 25 Youtube




3 Expand I X Y Z 2



How To Simplify Math X Y Z 2 X Y Z 2 X Y Z 2 X Y Z 2 Math Quora



Xyz Affair Amayah Granadosin Storyboard By F47c71b2




Expand Design 2k Function Real Statistics Using Excel



2
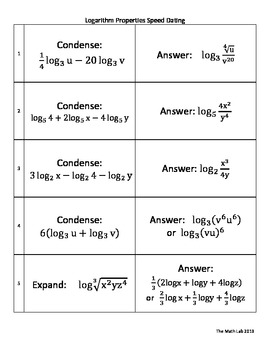



Logarithms Speed Dating Condensing And Expanding Activity By The Math Lab




3 Expand I X Y Z 2



Xyz Affair Storyboard By 859d9d7f




Xyz Enterprises Is Deciding Whether To Expand Its Production Facilities Although Long Term Cash Flows Are Difficult Homeworklib
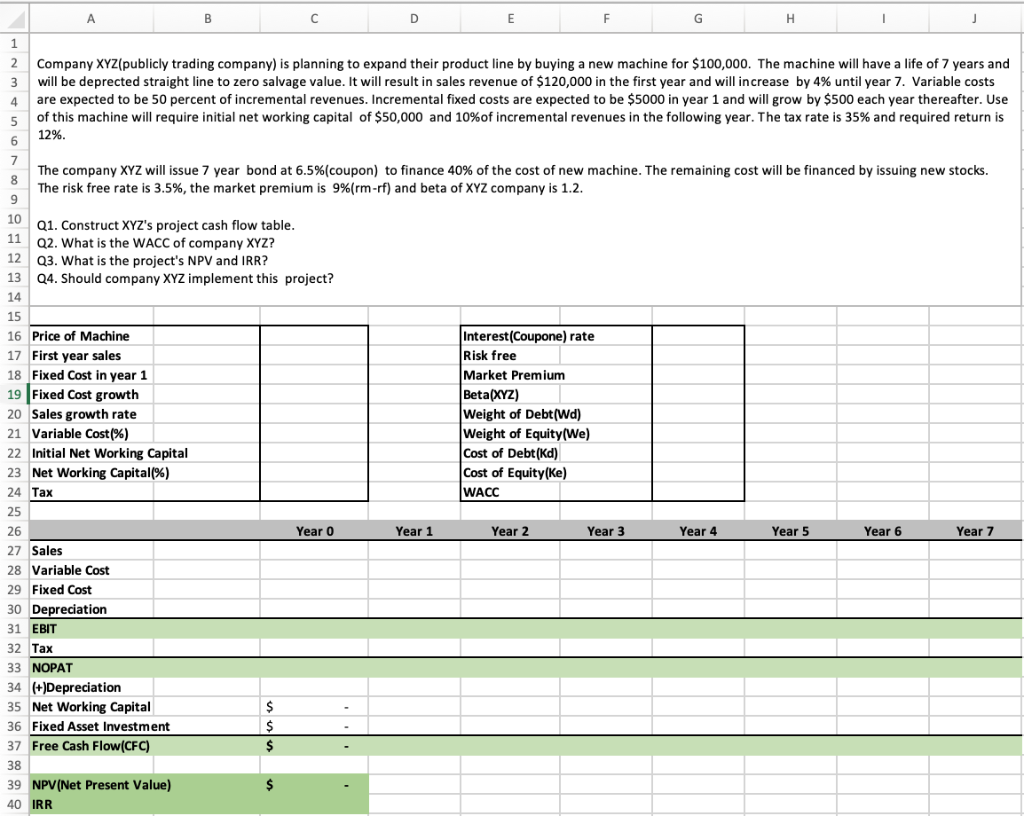



Company Xyz Publicly Trading Company Is Planning To Chegg Com




Gold Script Nameplate Necklace 3 Names Tiny s




Pdf A Review On Inventory Management Control Techniques Abc Xyz Analysis Semantic Scholar



Expand X Y Z Square Brainly In




Milling Machines Tools Home Improvement Genmitsu Cnc Router Machine Proverxl 4030 Xyz Working Area 400 X 300 X 110mm 15 7x11 8x4 3 24 X 24 Proverxl 4030 Xy Axis Extension Kit Upgraded Accessories Expand




Us Laser 3 Axis Xyz 3 1 Fixed Ratio Laser Beam Upcollimator Expander Ebay




Zeiss Humphrey Chin Rest Paper Pkg Of 100 Xyz Bernell Corporation




Xyz Footwear Is A Leading Footwear Company In India They Want To Exp




Principles Of Digital Design Chapter 3 Boolean Algebra And Logic Design Boolean Algebra Logic Gates Digital Design Implementation Technology Asics Ppt Download
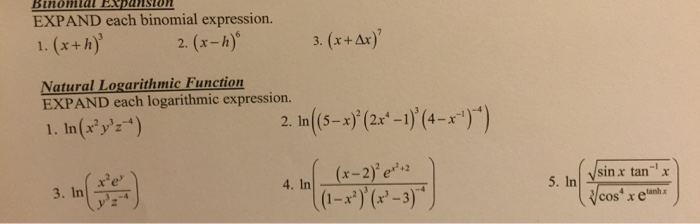



Solved Expand Each Binomial Expression X H 3 X H 6 Chegg Com




Paypal Checkout Can You Auto Expand The Cart Stack Overflow




Milling Machines Tools Home Improvement Genmitsu Cnc Router Machine Proverxl 4030 Xyz Working Area 400 X 300 X 110mm 15 7x11 8x4 3 24 X 24 Proverxl 4030 Xy Axis Extension Kit Upgraded Accessories Expand




Tukitaki Xyz Let Your Children Expand The Horizons Of Their Imagination With Storybooks That Would Encourage Them To Read More Tukitaki Xyz Page 3 Term Books Childrens S Post Type Product Taxonomy Product Cat Facebook
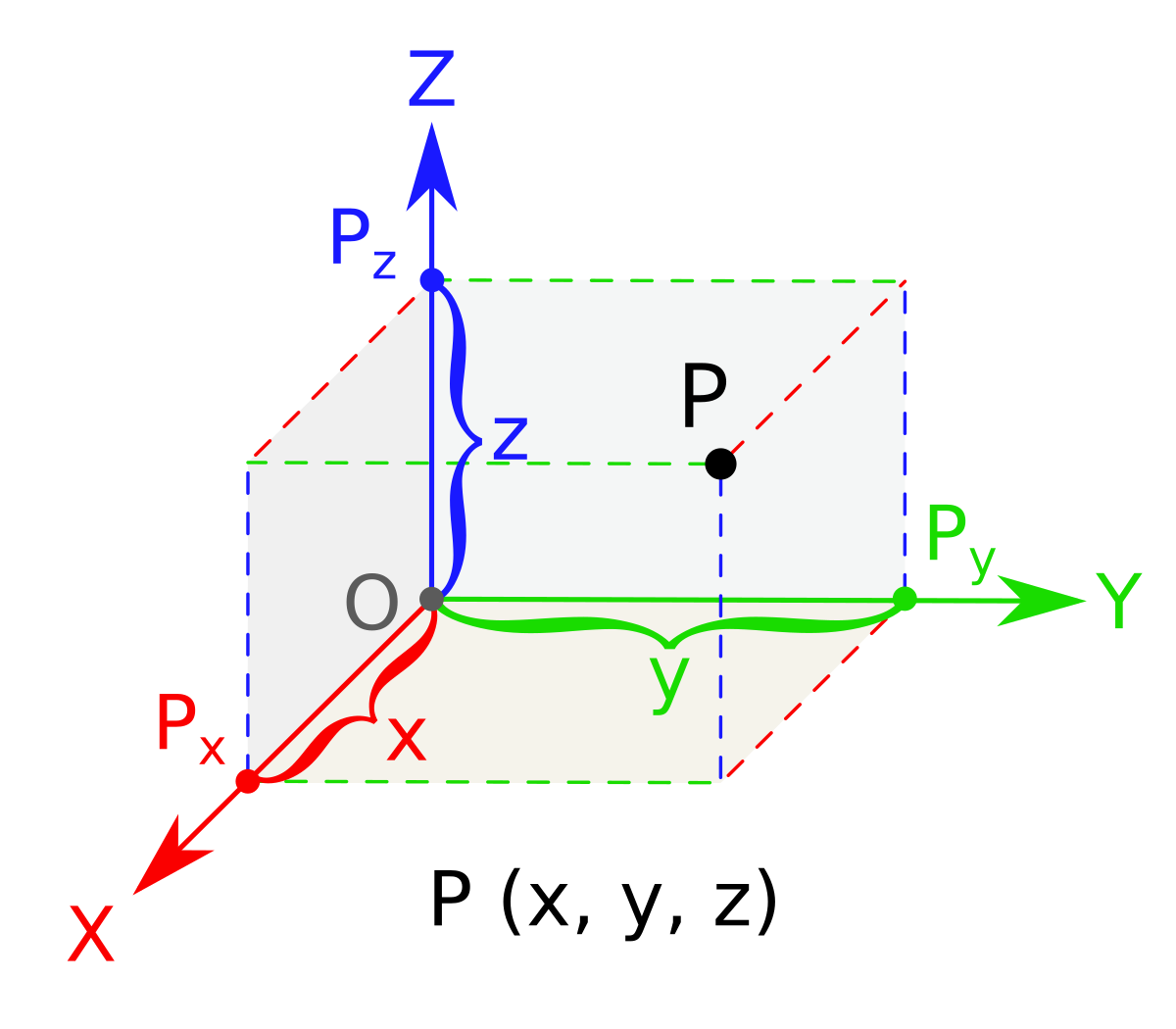



Three Dimensional Space Wikipedia




Project Overview Statement Pos




Xyz Is A Full Service Law Firm Aiming To Expand From Being A Lea Docx Xyz Is A Full Service Law Firm Aiming To Expand From Being A Leading Regional Course Hero




Milling Machines Tools Home Improvement Genmitsu Cnc Router Machine Proverxl 4030 Xyz Working Area 400 X 300 X 110mm 15 7x11 8x4 3 24 X 24 Proverxl 4030 Xy Axis Extension Kit Upgraded Accessories Expand




Milling Machines Tools Home Improvement Genmitsu Cnc Router Machine Proverxl 4030 Xyz Working Area 400 X 300 X 110mm 15 7x11 8x4 3 24 X 24 Proverxl 4030 Xy Axis Extension Kit Upgraded Accessories Expand
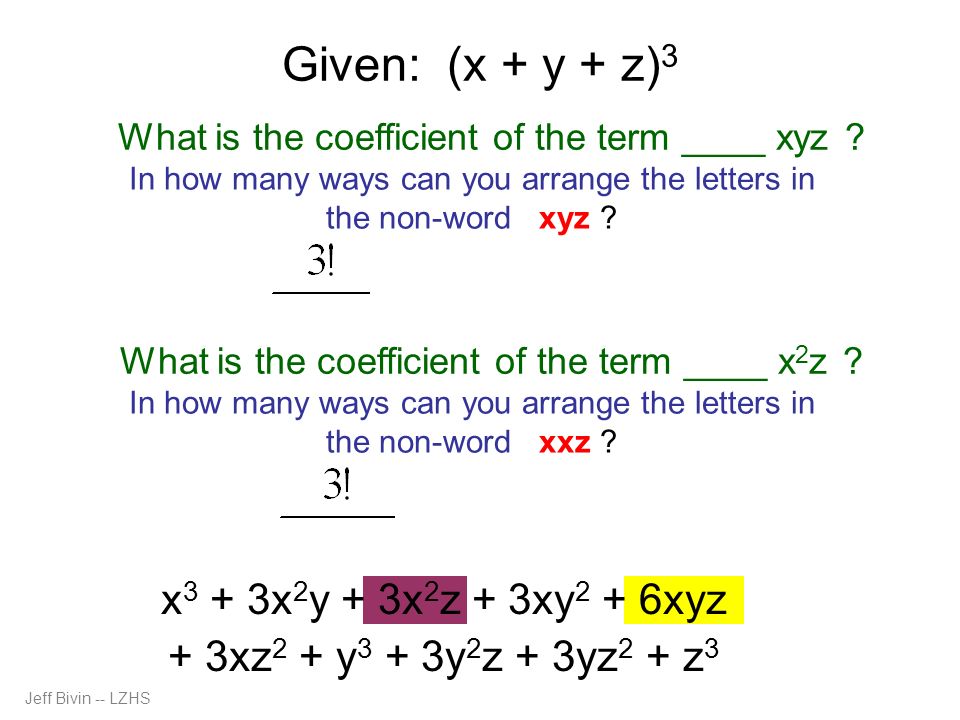



Binomial Expansion And More Ppt Download




Chapter 4 Expansion R K Bansal Solutions For Class 6 Mathematics Maharashtra Topperlearning




Xyz Link Otg Cable For One Plus 5 Type C To Usb Cable Oneplus 5 Type C Otg Cable For Cable For Otg Cableusb Cable Aliexpress




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube




Expand The Logarithm Log4 3xyz 2 Brainly Com



Yi5lzcfvajahcm




Nuair Land Expand In Central New York Stop By Booth 3331 Auvsishow To See Everything Cny Has To Offer Show Floor T Co Ihqeweiasl Centerstateceo Empirestatedev Geniusnyprogram Onegroupins Sentientblue Skyop Thalesusa



8th Pre Alg L40 Inv 4




Solved Calibri Bo A A V Po I 4 A A Paragraph D Paste Styles Rewrite Each Equation In Logarithmic Form 13 170 1 14 2561 2




Expand Number Of Rows By Column Count Vba Stack Overflow




Modular Xyz Xpansion Pins Mitee Bite Products Llc




Download Gravity Forms Expand Textareas 1 1 Xyz Theme




Expand Your Tool Box With New Toys




Xyz Reality Raises m To Build Ar For Construction Industry Sifted



Da Vinci Jr 1 0 A Pro 3d Printer




Expanded Form Of X Y Z 2 Is Brainly In




Equity Crowdfunding Pitch Deck Geographic Expansion Strategy Ppt Professional Display Pdf Powerpoint Templates




Expand Form Of X Y Z Whole Square Brainly In




Xyz Enterprises Is Deciding Whether To Expand Its Production Facilities Although Long Term Cash Flows Are Difficult Homeworklib




Fnce 3010 Durham Hw 18 Capital Structure




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube



I M Having Trouble Logging In What Do I Do




3d Tiskarna Xyz Da Vinci Nano W Pla 12x12x12cm 100 400 Mikronu Wi Fi Usb 2 0 30 Mm S 70 Mm S Ed System A S



Startup Presentation For Collaborative Capital Funding Geographic Expansion Strategy Pictures Pdf Powerpoint Templates




Top 10 Strongest Rank 10 Xyz Monsters In Yu Gi Oh Hobbylark




Japan To Expand State Of Emergency In 7 More Prefectures Social News Xyz



Expand The Given Logarithms 3 Points Each Log Frac Gauthmath




Milling Machines Tools Home Improvement Genmitsu Cnc Router Machine Proverxl 4030 Xyz Working Area 400 X 300 X 110mm 15 7x11 8x4 3 24 X 24 Proverxl 4030 Xy Axis Extension Kit Upgraded Accessories Expand




Xyz Reality Home Facebook




Modular Xyz Xpansion Pins Mitee Bite Products Llc




Find The Sum Of Products Expansions Of The Boolean Function F X Y Z That Equals 1 If And Only If A X 0 B Xy 0 C X Y




Solved 4 Expand The Following 3x 2 3 5 2 2 4 Chegg Com
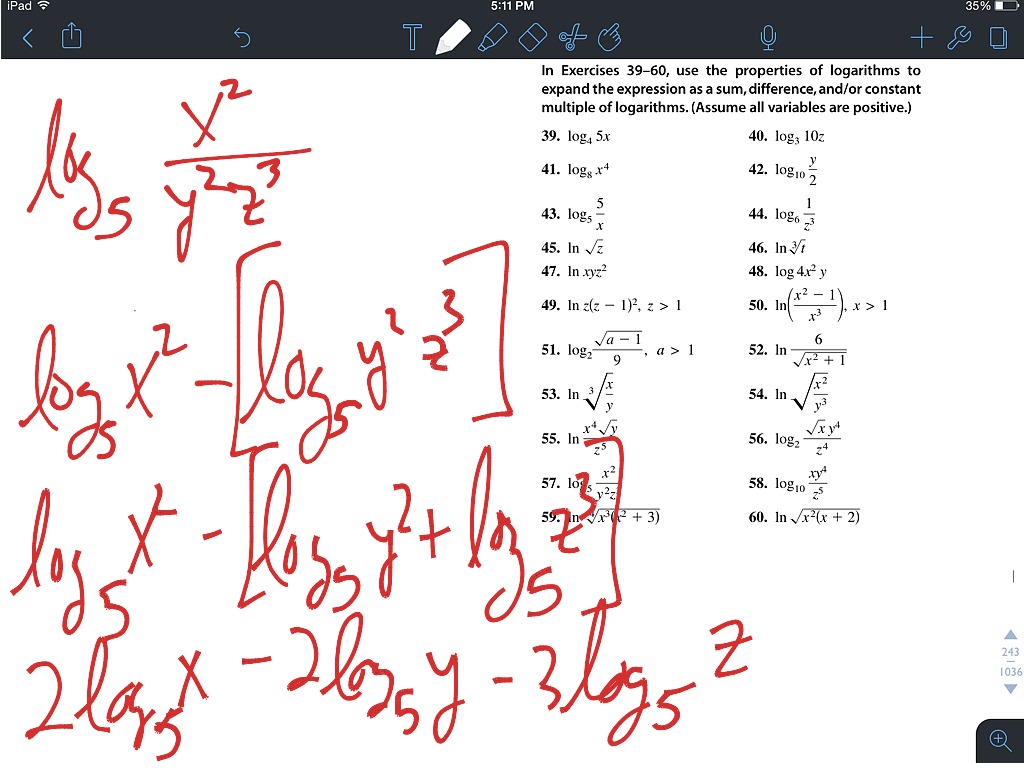



3 3 Expanding Logs Math Precalculus Logarithms Expanding Logarithms Showme
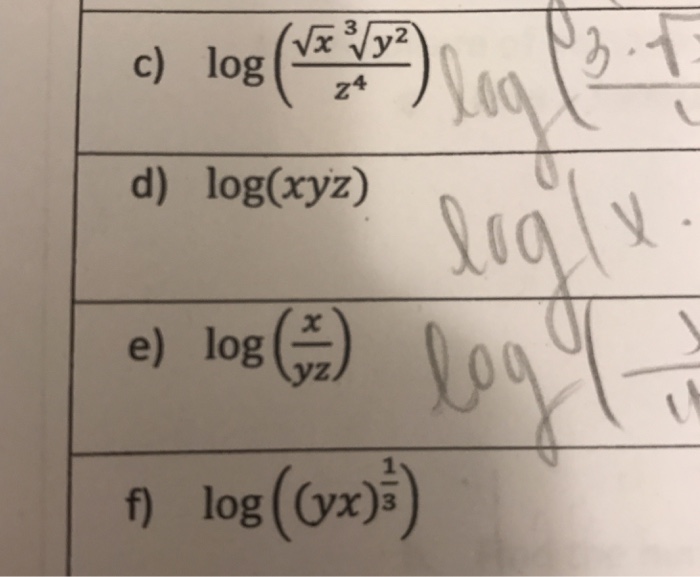



Solved For C And F How Do You Expand The Following Chegg Com




Example 32 Show That Determinant 2xyz X Y Z 3 Class 12



Trinomial Expansion



The Number Of Terms In The Expansion Of X Y Z N Studyrankersonline




Narsee Monjee Assignments March 21 Abc Bank Was A Domestic Bank And Was Doing Good In The Indian By Sales Casestudyhelp Issuu




Write The Expanded Form Of X Y Z 3 Brainly In



0 件のコメント:
コメントを投稿