Solution for F(x)= x^24 f(2)f(h)Eq1) or equivalently if the following equation holds for all such x f (x) − f (− x) = 0 {\displaystyle f(x)f(x)=0} Geometrically, the graph of an even function is symmetric with respect to the y axis, meaning that its graph remains unchanged after reflection about the y axis Examples of even functions are The absolute value x ↦ x , {\displaystyle x\mapsto x,} x ↦ x 2Δ = b 24ac Δ = 4 24·1·(1) Δ = The delta value is higher than zero, so the equation has two solutions We use following formulas to calculate our solutions

F Dfrac F Dfrac F D See How To Solve It At Qanda
If f(x)=4^x/4^x 2 then f(1/1997)
If f(x)=4^x/4^x 2 then f(1/1997)-Then the power of the x, the 3, reduces by one becoming a 2 Therefore, the result is 12x^2 You would then do the same thing for the remaining parts of the equation x^2 becomes 2x x^2 is the same as 1x^2 so we do the number in front multiplied by the power (1 2=2) and then reduce the power by one (21=1) Consider given function f(x) = 6x – 4 Now f(8) = 6(8) 4 = 48 4 = 44 Thus, the value of function f(x) = 6x – 4 when x= 8 is 44 johnsonlogr johnsonlogr Alphonso was earning S1,860 per month and then got a 12% raise How much will he make per month now?




If F X 4 X 4 X 2 Then F X F 1 X Is Equal To
We have a function given in this problem If we want, we can evaluate this function at a specific value for x The notation given, f(1), tells us𝑓(𝑥)=(4𝑥 − 3)6𝑥 − 4 𝑓(𝑓𝑥) = 4𝑓(𝑥) − 36𝑓(𝑥) − 4 𝑓𝑜𝑓𝑥 = 44𝑥 − 36𝑥 − 4 − 364𝑥 − 36𝑥 − 4Put x = y = z = 1 = 4*3 3A If = 4 (xyz) then find A = ?
Skill 1 Evaluating Functions Evaluating functions involves putting numbers into the function to get the result Example A function is given by f(x) = 3x1, Find f(10) All this requires is to replace x with 10 and calculate the result When we input 10 into this function that would look like f(\textcolor{red}{10}) = 3\times \textcolor{red}{10} 1 = 31If f (x) = x1/x1 then find the value of f (2x) Find the answer to this question along with unlimited Maths questions and prepare better for JEE examinationF(x1)=3x4 Which can be written as f(X1)=3(x1) 7 Hence, f(x)=3x 7 Therefore f(4)= 3*(4) 7 f(4)=12–7 f(4)=19
The Lagrange interpolation formula is a way to find a polynomial which takes on certain values at arbitrary points Specifically, it gives a constructive proof of the theorem below This theorem can be viewed as a generalization of the wellknown fact that two points uniquely determine a straight line, three points uniquely determine the graph of a quadratic polynomial, four points uniquelySal finds the inverses of f(x)=x4 and g(x)=2x1 Sal finds the inverses of f(x)=x4 and g(x)=2x1 opposite we solve for X in terms of Y so let's subtract 4 from both sides you get Y minus 4 is equal to negative x and then to solve for x we could multiply both sides of this equation times negative 1 and so you get negative y plus 4 isSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



2



Let The Function F 0 1 R Be Defined By F X 4x 4x 2 Then The Value Of F 1 40 F 2 40 F 3 40 F 39 40 F 1 2 Is Sarthaks Econnect Largest Online Education Community
We get rid of parentheses F1/F4=0 We multiply all the terms by the denominator F*F4*F1=0 We add all the numbers together, and all the variables 4FF*F1=0 Wy multiply elements F^24F1=0 a = 1;Create your account View this answer The given function is f(x) = 4x−3 f ( x) = 4 x − 3 We can assume that y = 4xTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `2f (x1)f((1x)/x)=x , then f(x)` is
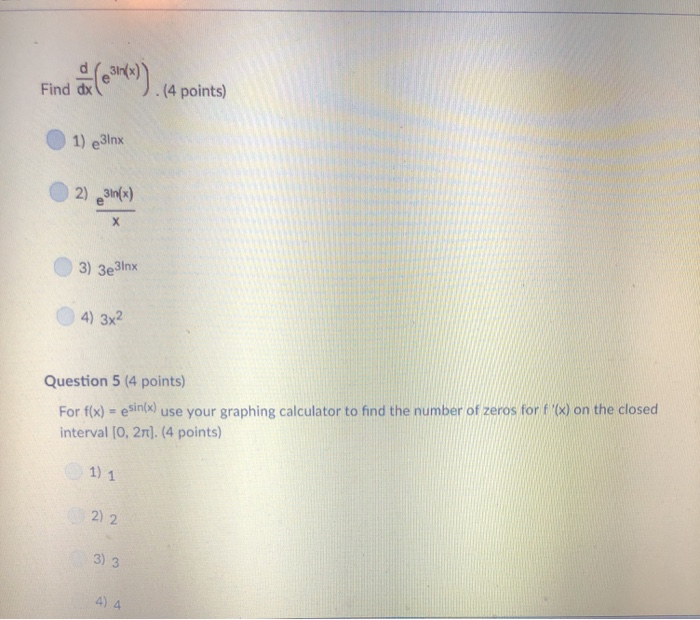



Solution If Fx 7x6cos1x Find F X 4 Points 1
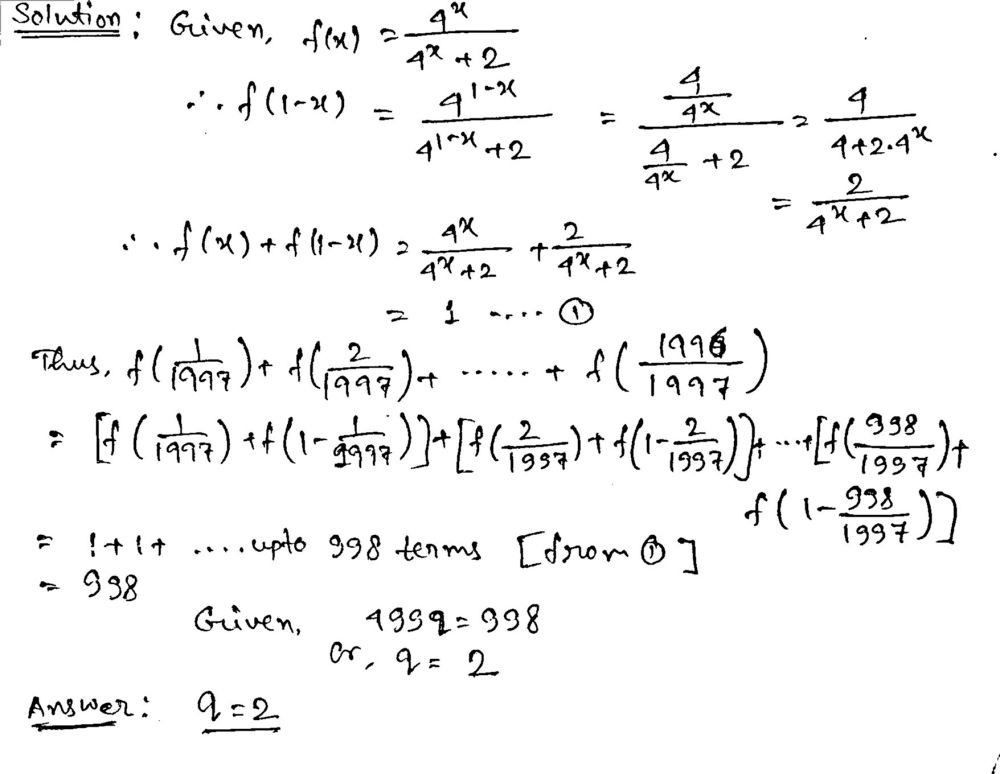



Consider F X Frac 4 X 4 X 2 If F Frac 1 1997 F Frac 2 1997 Dots F Frac 1196 1997 499q Then Q Is Equal To Snapsolve
Explanation Using the defined function, f(a) will produce the same result when substituted for x f(a) = a 2 – 5 Setting this equal to 4, you can solve for a a 2 – 5 = 4 a 2 = 9 a = –3 or 3F (x) = 4x24x f (4−x) = (4x2)2 f (x)f (1−x) = 1f ( )f ( ) = 1,f ( )f ( ) = 1⇒ sum = = 998 and so onDetermine composite and inverse functions for trigonometric, logarithmic, exponential or algebraic functions as part of Bitesize Higher Maths



Http Mswilliamswebsite Weebly Com Uploads 1 3 4 7 June 14 Practice Regents Pdf



Http Mswilliamswebsite Weebly Com Uploads 1 3 4 7 June 14 Practice Regents Pdf
View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn If f(x) =(4x3/6x4), x ≠ 2/3 1 Show that fof{x)=x, for all x ≠ 2/3 2 What is the inverse of 'f? Add 1 to both sides y 1 = 4x Divide both sides by 4 y 1 4 = x Where ever there is a x write y and wherever there is a y write x y 1 4 = x is changed to x 1 4 = y = f −1(x) f −1(x) = x 1 4 Answer link




F R R Is Given By F X A X A X A Xe R Then F 1 1997 F 2 1997 F 1995 1997 F 1996 1997




If F X X 2 Then F F X At X 4 Is
Integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;The inverse function of y=4/(x1) can be found by changing x to y and y to x, then solve for y So x=4/(2y1) Crossmultiply to get x(2y1)=4 Divide both sides by x to get 2y1=4/xWhen f(x)=x^42x^33x^2axb is divided by x1 andx1,we get remainders 19 and 5 respectivelyfind the remainder when f(x)is divided by x3 Get the answer to this question by visiting BYJU S Q&A Forum
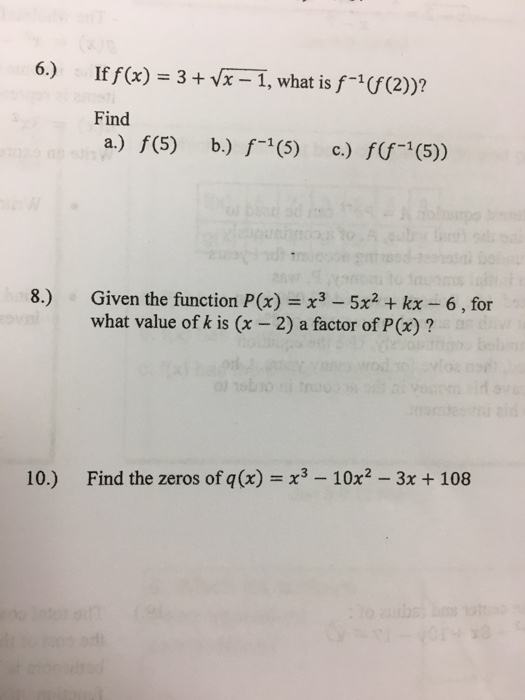



If F X 3 Squareroot X 1 What Is F 1 F 2 Chegg Com




Let F X 4 X 4 X 2 And Given That F X F 1 X 1 Then F 1 1997 F 2 1997 F 3 1997 F 1996 1997 Is
Graph f(x)=(1/4)x Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the form The slope of the line is the value of , and the yintercept is the value of 102 A marathon is 262 miles long There is a water station every 1 1/4 miles along the race route How many water stations are needed for this marathIf f (x) = 4^x/4^x 2, f (x) f (1 x) = a and f (1/97) f (2/97) f (96/97) = b then order pair (a,b) is




Let F X 4 X 4 X 2 And Given That F X F 1 X 1 Then F 1 1997 F 2 1997 F 3 1997 F 1996 1997 Is




Let F X 9 X 9 X 3 Then Find The Value Of F 1 06 F 2 06 F 3 06 F 05 06 Youtube
Integrate 1/(cos(x)2) from 0 to 2pi; If f is a function such that f(0) = 2, f(1) = 3 and f(x 2) = 2f(x) − f(x 1) ∀ x ∈ R, then f(5) is asked in Sets, relations and functions by SudhirMandal ( 536k points) sets9 Let f be a continuous real function on R1, of which it is known that f 0(x) exists for all x 6= 0 and that f (x) → 0 as x → 0Dose it follow that f0(0) exists?




What Is The Answer If F X 4x 7 Find F 1 X Quora



Http Www Gallup Unm Edu Smarandache Snbook11 Pdf
This example uses the basic function \(y = f(x)\) This can then be uses to draw related functions Notice that the main points on this graph are \(x = 2,\,1,\,4\) Graph of y = f(x) kIf f(x) is a product of several factors, any constants (terms in the product that do not depend on x) can be omitted For example, let f(x) = 6x 4 − 2x 3 5, and suppose we wish to simplify this function, using O notation, to describe its growth rate as x approaches infinity This function is the sum of three terms 6x 4, −2x 3, and 5F(x) f(1x) = 4 x /(4 x 2) 4 1x /(4 1x 2) = 4 x /(4 x 2) 2/(4 x 2) = 1 So f(1/97)f(96/97) = f(1/97) f(11/97) = 1 Similarly f(2/97)f(95/97) = 1 So the required sum = times Henct the required sum = 48




If F X Then What Is The Value Of F 1 1996 F 2 1996 F 1995 1996 Mathematics Topperlearning Com Zl5v8gff




Suppose F Is Continuous On 0 00 A If F 1 Chegg Com
1 Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of Transcript Misc 2 If f(x) = x2, find (𝑓(11) − 𝑓(1))/((11 − 1 ) ) Let us first find f(11) and f(1) For f(11) f(11) = (11)2 = 11 × 11For example, we can multiply the functions f(x) = 1/ x and g(x) = 2 as, The domain of the ( f g )( x ) consists of all x values that are in the domain of both f and g In this example, f has domain { x x ≠ 0}, and g has domain all real numbers, therefore ( f g )( x ) has domain { x x ≠ 0}, because these values of x are in the domain of both f and g



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf
1 2 f00(ξ)(x 1 −x 0) Here, we simplify the notation and assume that ξ ∈ (x 0,x 1) If we now let x 1 = x 0 h, then f0(x 0) = f(x 0 h)−f(x 0) h − h 2 f00(ξ), which is the (firstorder) forward differencing approximation of f0(x 0), (53) Example 52 We repeat the previous example in the case n = 2 and k = 0 This time Q 2(x) = fIntegrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Formula of polynomials If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____




If F X 4 X 4 X 2 Then F X F 1 X Is Equal To



Http Www Newpaltz K12 Ny Us Cms Lib Ny Centricity Domain 98 Midterm practice 18 Pdf
Answer and Explanation Become a Studycom member to unlock this answer!If f(x)=(x4/2√x), then f'(1) is (A) (5/4) (B) (4/5) 1 (D) 0 Check Answer and Solution for above question from Mathematics in Limits and Deriva f^(1)(x) = sqrt(x4) We have f(x) = x^24 And we seek the inverse function, f^(1)(x) My preferred approach is to put y = x^24 A And rearrange to form an explicit relationship x=f(y), and this function is the inverse, f^(1)(x) So, from A we have x^2 = y4 x = sqrt(y4) Thus f^(1)(x) = sqrt(x4) Note that by the formal definition f^(1)(x) is not a



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf



If F 3 F 3 F 3 3 And F X 0 What Is F 1 Quora
The function f is defined by f (x) = x4 −4x2 x 1 for −5 ≤ x ≤ 5 What is the interval in which the minimum of value of f Purely a graphical approximation;Simple and best practice solution for f(x)=2(x2)(x4)4 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?




Solved If F X 1 9 X 2 What Is F 1 X Brainly Com




Pre Algebra A Practical Step By Step Approach
Given a function g with this property, we can easily construct a suitable f Just let f ( x) = { g ( x) x ≥ 0 g ( − x) x < 0 If g is additionally continuous then so is f We can find a lot of continuous g Pick a 1 ∈ ( 0, 1), let a 0 = 0 and recursively a n = a n − 2 2 1 for n ≥ 2A (xyz)2 B x2y2z2 C xyyzzx D x2y2z2xyyzzx Please scroll down to see the correct answer and solution guideFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




If F X 4 X 4 X 2 Then F X F 1 X Is Equal To
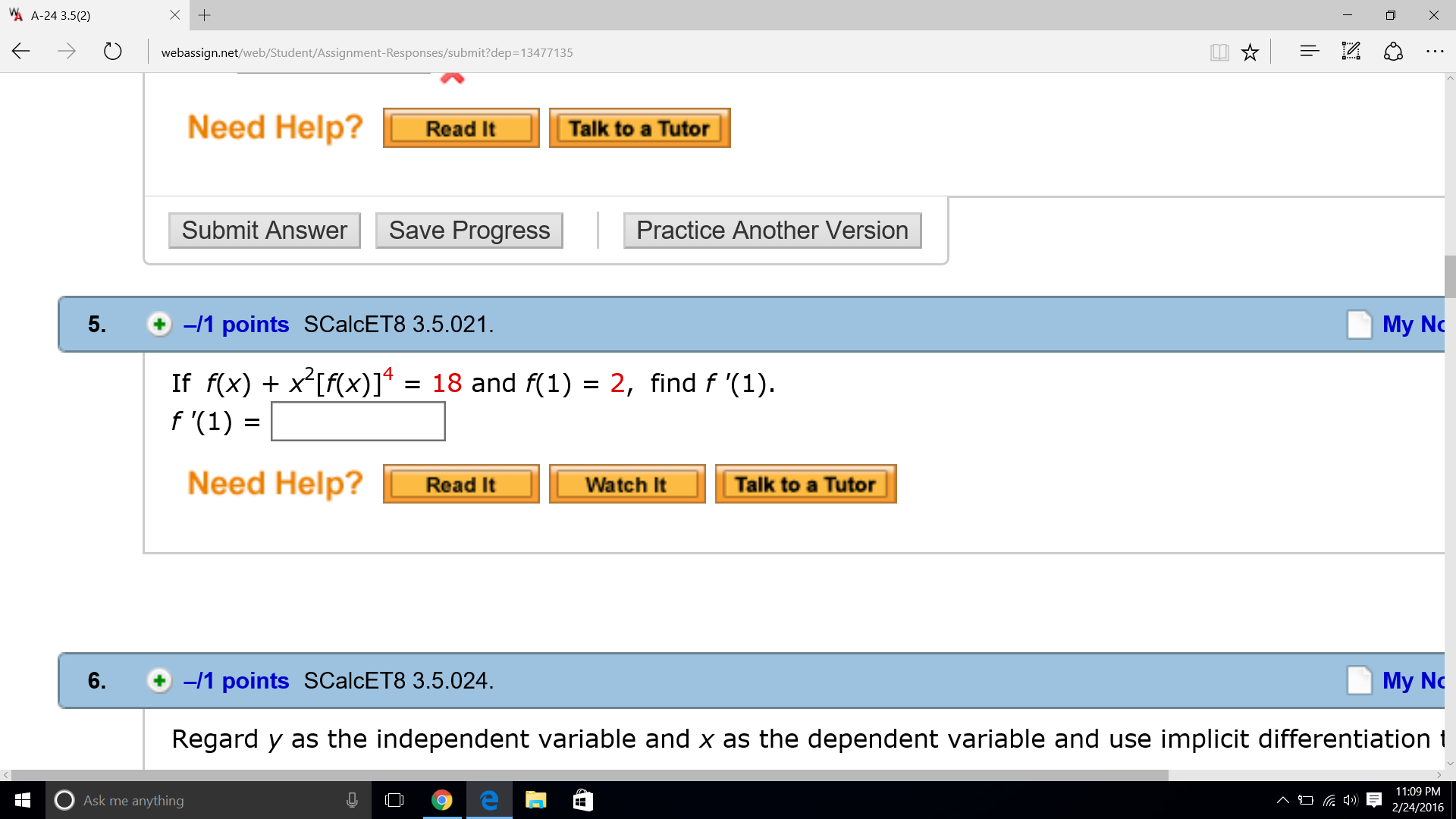



If F X X 2 F X 4 18 And F 1 2 Find F 1 F 1 Chegg Com
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `if f(x)f(1/x)=f(x)f(1/x) and f(3)=28` Then find f(4)When you wrote f1(x), did you mean the inverse function of f(x)?Minimum f = 463, nearly This is improved to 8sd, \displaystyle {} , using an iterative numerical method



2



Http Www Math Northwestern Edu Mlerma Problem Solving Putnam Training Problems 11 Pdf
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeTo meet its production orders, the warehouse of Basic Office Supplies has to Ex13 , 4 If 𝑓(𝑥)=(4𝑥 − 3)6𝑥 − 4, 𝑥 ≠ 23 , show that 𝑓𝑜𝑓(𝑥)=𝑥, for all 𝑥 ≠ 23 What is the inverse of f?



Www Silsbeeisd Org Site Handlers Filedownload Ashx Moduleinstanceid 5566 Dataid 3564 Filename 10 taylor series and error bounds Pdf



Www Bauer Uh Edu Rsusmel 4386 09 18 Ch 08 Pdf
Composite Functions – Explanation & Examples In mathematics, a function is a rule which relates a given set of inputs to a set of possible outputs The important point to note about a function is that each input is related to exactly one output The process of naming functions is known as function notation TheNote We prove a more general exercise as following Suppose that f is continuous on an open interval I containing xIf f X!Y is continuous and V ˆY is closed, then f 1(V) is closed Another good wording Under a continuous function, the inverse image of a closed set is closed



Igor Kortchemski Perso Math Cnrs Fr Olympiades Problemes Mc96 97 01feb Pdf




First Find F And Then Find F F X 3x3 4x2 2x Chegg Com
6 Simplified Dirac identities Figure 1The "picket fence representation" (5) of f(x),compared with the "stacked slab representation" (6) Partialintegration




If F X X 1 X F 1 5 2 Then F X Youtube




If F X Is Defined As Follows Find A F 2 B Chegg Com
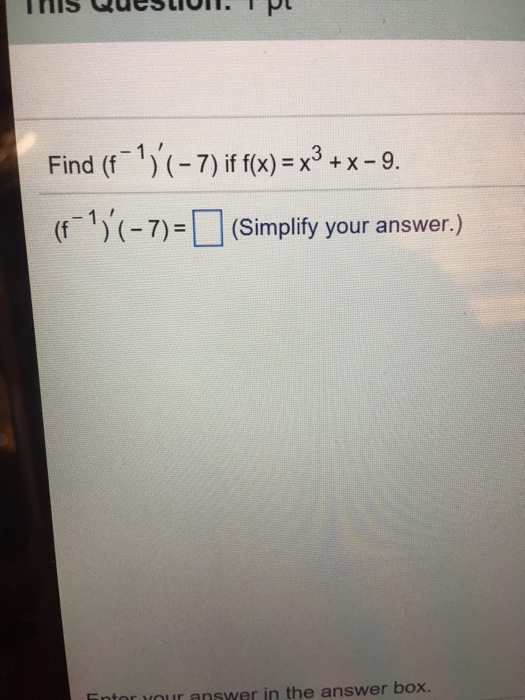



Find F 1 7 If F X X 3 X 9 F 1 7 Chegg Com




F Dfrac F Dfrac F D See How To Solve It At Qanda




If F X 4 X 4 X 2 Then F X F 1 X Is Equal To



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf




Find The Derivative Of The Function F X X Chegg Com




If The Function F R R Defined By F X 4 X4 X 2 Then Show That F 1 X 1 F X And Hence Deduce The Value Of F 14 2f 12 F 34




Let F X 4 X 4 X 2 Then Value Of F 1 1997 F 2 19




Let F X 9 X 9 X 3 Then Find The Value Of F 1 06 F 2 06 F 3 06 F 05 06 Youtube
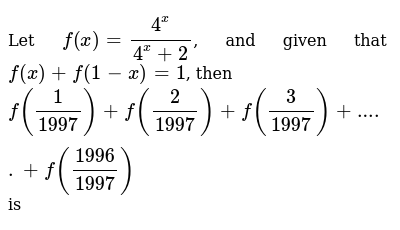



Let F X 4 X 4 X 2 And Given That F X F 1 X 1 Then F 1 1997 F 2 1997 F 3 1997 F 1996 1997 Is



2




If F X 4 X 4 X 2 1 For All X Belongs To R Then F 1 1997 F 2 Askiitians




If F X Find F 0 F 1 F 4 F 5 F 0 Chegg Com



Q Tbn And9gcqyaq8hkivm1bbia5ltn0sygm4j18hnwuxjljfo92usudjjkejf Usqp Cau




Consider The Function 𝑓 𝑥 𝑥 4 F X X Chegg Com




A The Function F X Is Defined By F X Rightarrow Chegg Com




If F X 1 X X 4x 8 Then F X 1 Brainly In
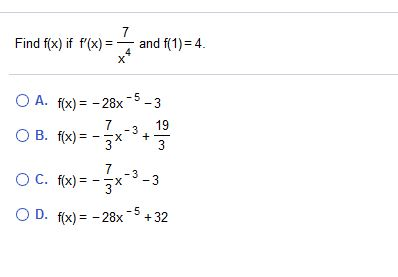



Find F X If F X 7 X 4 And F 1 4 A F X Chegg Com




If F X 2x 6 3x 4 4x 2 Then F X Is
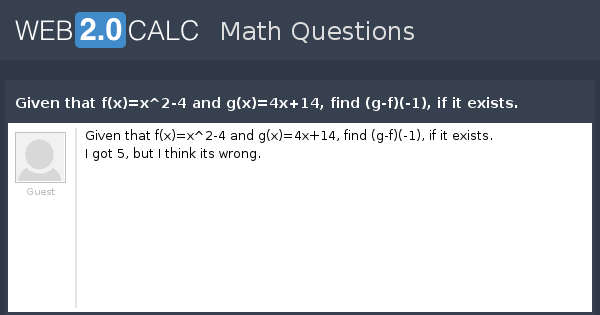



View Question Given That F X X 2 4 And G X 4x 14 Find G F 1 If It Exists



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf



Www Jstor Org Stable




Given F X 3x 6 Find F 1 X Then State Whether F 1 X Is A Function Brainly Com




Jee Mains 18 A Real Valued Function F X Satisfies The Functional Equation F X Y F X F Y Youtube



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf
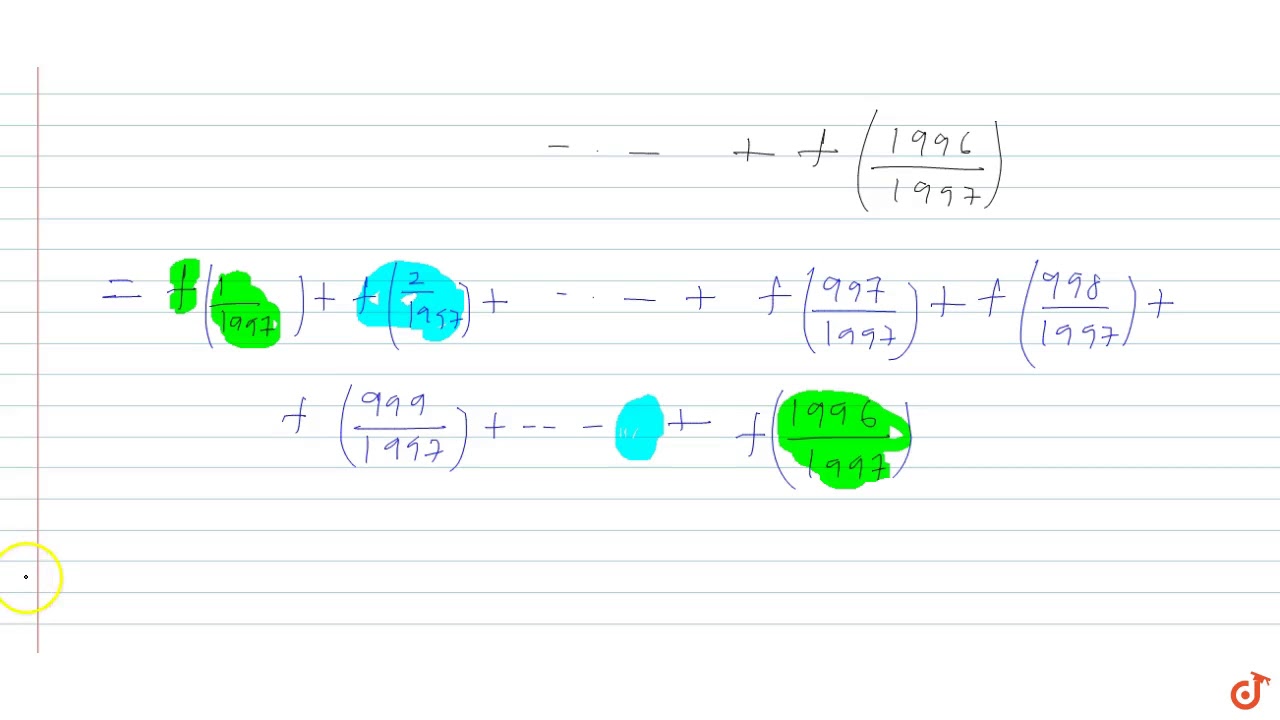



Let F X 4 X 4 X 2 And Given That F X F 1 X 1 Then F 1 1997 F 2 1997 F 3 1 Youtube



Http Www Mrdengsmathclasses Com Uploads 2 3 9 2 14 6 Answers Pdf




Mega Man X4 Wikipedia



Www Cbsd Org Cms Lib Pa Centricity Domain 92 1997 mc exam solutions Pdf




Shallow And Deep Neural Network Training By Water Wave Optimization Sciencedirect



Http Mswilliamswebsite Weebly Com Uploads 1 3 4 7 June 14 Practice Regents Pdf



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Theorems Pdf




If F X X 2 F X 4 18 And F 1 2 Find F Chegg Com



Q Tbn And9gcsmm4ktmxrxm10kmsg3wqo5rzire Ogwbm0v2tajixhbesgniod Usqp Cau



F X X



Show That A Function F R R Given By F X Ax B A B R A 0 Is A Bijective Sarthaks Econnect Largest Online Education Community



Www Jstor Org Stable



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Theorems Pdf




If F X 4 X 4 X 2 1 For All X Belongs To R Then F 1 1997 F 2 Askiitians




Let F X 4 X 4 X 2 Then Value Of F 1 1997 F 2 19



Www Rhnet Org Site Handlers Filedownload Ashx Moduleinstanceid 6070 Dataid Filename Alg Intro To Functions Unit Review Pdf



Http Abel Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf




If F X 4 X 7 3 Then F 1 X




Let F X 04 30if X Lt 3if 3 X Lt 0if Chegg Com




If F X 9 X 9 X 3 Then F 1 1996 F 2 1996 F 1995 1996 Youtube



Cdanfort W3 Uvm Edu Courses 19 Waner Solutions Pdf




If F 1 10 And F X 2 For 1 X 4 How Small Can F 4 Poss Quizlet




Let F X 4 X4 X 2 Then The Value Of F F F




If F 1 0 And F 1 1 What Can You Say About Chegg Com



Http Mswilliamswebsite Weebly Com Uploads 1 3 4 7 June 14 Practice Regents Pdf




If F X 4 X 7 3 Then F 1 X Youtube
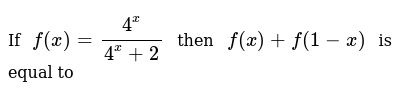



If F X 4 X 4 X 2 Then F X F 1 X Is Equal To



Www Jstor Org Stable




Which Of The Following Is The Function F X If F 1 Y Y 8 3 Picture Attached Brainly Com




If The Function F R R Be Given By F X X 2 2 And G R R Be Given By G X Xx 1 X 1 Find




A New 5d Hyperchaotic System With Stable Equilibrium Point Transient Chaotic Behaviour And Its Fractional Order Form Springerlink
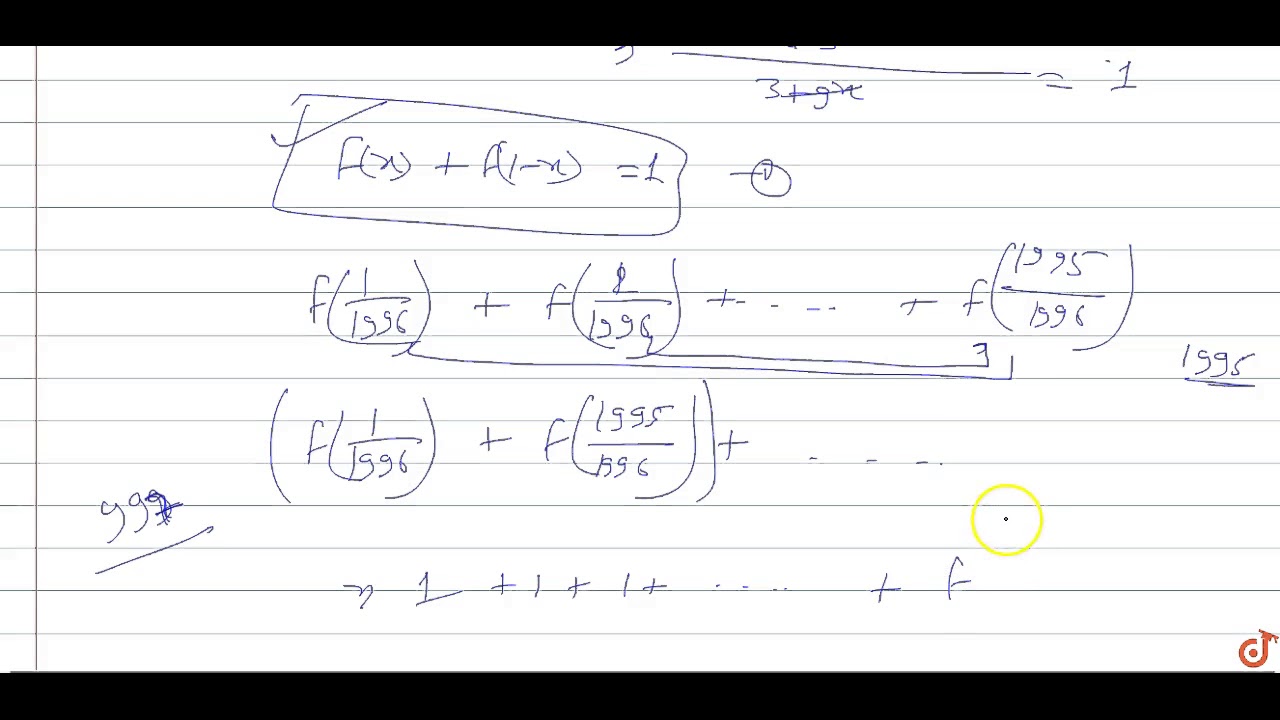



If F X 9 X 9 X 3 Then F 1 1996 F 2 1996 F 1995 1996 Youtube




Let F X 4 X 4 X 2 And Given That F X F 1 X 1 Then F 1 1997 F 2 1997 F 3 1997 F 1996 1997 Is




40 If F X Frac 4 X 4 X 2 Then F Left Frac 1 1997 Right F Left Frac 2 1997 Right Ldots F Left Frac 1996 1997 Right Text Is Equal To Begin Array Ll Text A 1997 Text B 998 Text C 0 Text



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Theorems Pdf



Http Mswilliamswebsite Weebly Com Uploads 1 3 4 7 June 14 Practice Regents Pdf




If F X 4 X 4 X 2 1 For All X Belongs To R Then F 1 1997 F 2 Askiitians




Dubey
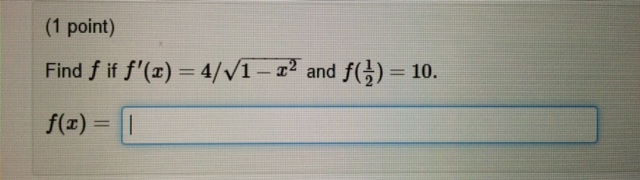



Find F If F X 4 1 X 2 And F 1 2 10 F X Chegg Com



Www Jstor Org Stable




Classify The Following Functions F X Defined In Mathbb R Rightarrow Mathbb R As Injective Surjective Both Or None N Begin Array L L L L



Math Berkeley Edu Corteel Math249 08 0 Pp 286 560 Symmetric Functions Pdf



Inverse Functions



If F X 2 How Can You Find F 0 And F 2 Quora




Hongkong Olympiad Flip Ebook Pages 501 550 Anyflip Anyflip



Www Jstor Org Stable



0 件のコメント:
コメントを投稿